Im Magazin „8000 PLUS" wurde im Juli 1989 der folgende Artikel abgedruckt.
(Im August 1989 folgten einige zusätzliche Hinweise)

Ein BASIC-Programm als Beispiel für das Plotten am PCW

SURFACES

by A M Baldwin

Mathematics can be a thrill. All over the world pictures which seem to be purely art pour l'art are being created. Not by impoverished artists but by well-funded scientists with powerful computers. These pictures bring to life previously abstract mathematical concepts — for example, the dimensions of unseen stars and even the effects of entropy on the universe. Already with the Mandelbrot set exploration printed in issue 31, these pages have shown how the PCW can help you foray into these rarified realms.

A M Baldwin's Surfaces program follows on from this new tradition by creating visual images of such mathematical functions as 5*(x/y+x)+EXP(-x*Y).

It achieves this by using Larry Simon's Plot routine (which is included in the listing - so you've got it yet again), first printed in issue 23 (raw sold out) and updated last month. The image produced consists of a series of graphs drawn one behind the other. The program then turns your PCW into a kind of roving microscope allowing you to view the image from some startling perspectives. For example you can look down from 'on high' or even delve around inside the shape. To do any of this you'll need to provide values for the variables listed below:

FNz: here the variable z represents the model function from which the drawing is taken. Changing the sign within the function changes the perspective. Signs such as COS or SIN will provide a wider view but some interesting distortions can also be obtained.

ed: this stands for Eye Distance. The greater the value assigned to ed the further your 'eye' is from the image. This creates a smaller, less detailed picture on the screen. Setting ed at 100 will normally give a good overall view of any shape; you can then pick areas to examine more closely.

sf: this stands for Scaling Factor. A more apt description might be magnification. The greater the value, the higher the magnification and the larger the image. A scaling factor of between 400 and 900 will produce reasonable detail, but as usual you should experiment.

st: this stands for STEP and is used with the FOR...NEXT loops throughout the program. st actually provides the area to be magnified. Setting st at 0.1 will give a fairly clear image quickly. A setting of 0.5 combined with an ed setting of 100 should give a good general sketch. A small value for st gives a small area to be magnified.

ax and az: these give the angles from which you view the shape. ax gives the up (high value) and down (low value). ax=0 is directly 'above' the image while ax=90 is 'ground level'. az, on the other hand, rotates the image. az=90 views the image 'straight on'. Anything above 90, or the use of negative numbers, will produce very little on the screen.

In order to change the values assigned to any of these variables you need to edit the relevant lines before running the program. You will probably find that this constant stopping and starting becomes a pain. A quick glance at the INPUT command in the Mallard Basic manual should provide you with a more convenient method ot assigning values.

The program, as it stands, is an impressive piece of work. It makes imaginative use of the Plot routine but it could always be modified. For example, might there be a way of having several shapes on the screen at once? Would it be possible to elongate or even crunch shapes? Why not try to answer these questions and when you've done that, send the solutions into us.

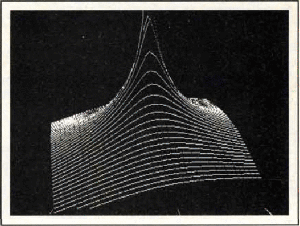
This was produced by the listing you are about to type in.

A few minor changes to the values of ed and and ax/az will produce this 'wave farm'.

The various variables are set up here. Line 40 converts the angles from degrees (which humans understand) into radians (for the computer).
Die Anweisung POKE 441,0 (Adresse 441 ist &1B9) unterdrückt die Ausgabe 'Ok' bei den Mallard BASIC Versionen 1.29 und 1.47.

The flags noted in lines 90 and 110 stop the PCW from drawing the return lines over lines already drawn.

190 tx=sx:ty=sy:NEXT x,y:PRINT e$"e":END                                       15D8
200 a%=INT(tx):b%=INT(ty)                                                      0B63
210 IF a%<0 OR a%>719 OR b%<0 OR b%>247 THEN 240                               11D4
220 IF b%<h(a%) THEN 240                                                       07FD
230 CALL plot(a%,b%):h(a%)=b%                                                  0BA2
240 RETURN                                                                     0507
250 ex=x*v1+y*v4:ey=x*v2+y*v5+z*v7:ez=x*v3+y*v6+z*v8+ed                        1C08
260 sx=ex*sf/ez+xc:sy=ey*sf/ez+yc:RETURN                                       16C8
270 MEMORY &HBFFF:plot=&HC000:a=plot:e=0                                       1496
280 RESTORE 400                                                                06D9
290 FOR f=0 TO 14                                                              0722

This section compares the values raised throughout the program to the boundaries of the screen. Numbers which go above screen limits are rounded down.

300 s=0                                                                        02B3
310 FOR g=0 TO 7                                                               06A5
320 READ x$:x=VAL("&H"+x$)                                                     0A03
330 s=s+x:POKE a,x:a=a+1:NEXT                                                  1055
340 READ x$                                                                    0401
350 IF s>>VAL("&H"+x$) THEN e=e+1:PRINT "Error in Line";10*(f+40)              1C03
360 NEXT                                                                       0428
370 IF e=0 THEN RETURN                                                         0ADD
380 PRINT e; "ERROR";:IF e=1 THEN PRINT ELSE PRINT "s"                         19C7
390 STOP                                                                       0461

Here the program reads the DATA lines which follow. Line 350 is an aid to debugging and informs you if you have made a mislake typing the DATA in.

400 DATA 0A,32,7C,C0,4E,23,46,21,250                                           0B8A
410 DATA CF,02,A7,ED,42,D8,ED,43,4AF                                           0E06
420 DATA 78,C0,EB,5E,23,56,7A,A7,41B                                           0CF8
430 DATA C0,93,3D,5F,ED,53,7A,C0,469                                           0D2A
440 DATA F3,ED,73,7D,C0,31,9D,C0,51E                                           0DEA
450 DATA 01,36,C0,CD,5A,FC,E9,00,403                                           0CBF
460 DATA ED,7B,7D,C0,FB,C9,2A,7A,50D                                           0E03
470 DATA C0,29,11,00,B6,19,5E,23,24A                                           0C8F
480 DATA 56,7B,E6,F8,CB,27,CB,12,47E                                           0DF5
490 DATA 47,7B,E6,07,B0,5F,2A,78,360                                           0CDB
500 DATA C0,45,7D,E6,F8,6F,EB,19,4D3                                           0DD0
510 DATA 78,E6,07,3C,47,AF,37,1F,2ED                                           0D89
520 DATA 10,FD,47,3A,7C,C0,A7,20,391                                           0CD6
530 DATA 05,78,2F,A6,77,C9,3D,78,347                                           0CBD
540 DATA 20,03,B6,77,C9,AE,77,C9,407                                           0C86
</form>

As always with programs which draw on the PCW screen there have to be DATA lines. These actually produce the Plol routine for Surface.Bas.

[BASIC-Listing] und [Assembler-Listing]

Getting Below the Surface

Last month we published Surface.bas, a program by Mr M A Baldwin. Following this we received a number of amendments from that same gentleman. Although the program as printed will work, the additions will add to its charms and provide even more pleasure. The points to note are as follows:

The variable st does stand for Step but will not provide the area to be magnified. To achieve this you will need to alter the parameters ot the loops in lines 90 and 100. What st does is to alter the frequency with which the lines are drawn within the area selected by the loops.
The POKE 441,0 in line 80 gets rid of the ok prompt. To get it back you will need to POKE 441,79.
Mr Baldwin suggests a number of functions which might produce some interesting images. The four listed below are just a selection ot those possible:
LOG(SQR(x*x+y*y))
-SIN(x*y)
SIN(x*y)
-SIN(SQR(x*x+y*y)x*y))
The lower illustration on page 61 is in fact the image of the function SIN(x*y) and is not achieved merely by altering the variables ed, ax and az. Many thanks again to Mr Baldwin for his program and apologies for our errors.