Im Magazin „ BYTE" wurde in der Ausgabe Januar 1977 der folgende Artikel abgedruckt.
Ein grundlegender Aufsatz zum Thema Hashing.
|
Ein Hash-Wert (dt. Streuwert) ist ein Wert, der aus einer komplexeren Datenstruktur (z.B. Zeichenketten) mittels einer Hash-Funktion berechnet wird.
Die Bedeutung dieses Informatik-Begriffes liegt darin, dass diese Zuordnung möglichst eindeutig ist, so dass Hash-Werte als Schlüssel für Tabellen benutzt werden können.
|
[Ein praxisnaher Artikel mit einem BASIC-Programm zu diesem Thema findet sich hier]
|
|
Making Hash With Tables
|
Terry Dollhoff
504 Early Fall Ct
Herndon VA 22070
|
Hashing ist eine Technik zum schnellen Suchen in Tabellen, wobei die Position in der Tabelle abhängig ist von den Daten.
Viele Programmierneulinge lehnen diese Technik ab, weil sie diese für allzu kompliziert halten, nur angewandt von Entwicklern exotischer Systemprogramme - aber das ist nicht der Fall.
Ein beliebig großes Programm, ob
Hashing is a technique used to speed up table searching operations by making position
in the table depend upon the data.
Many newcomers to programming reject hashing as an overly complicated technique useful
only by the designer of exotic systems software, but this is not the case.
Any large program, written for fun or profit, may include tasks of accessing, storing,
or modifying entries in a table or array.
Most game playing programs include a number of such tasks.
Application of hashing techniques can often dramatically improve the performance of these programs.
This article will explore the use of hashing (sometimes called key-to-address transformation)
as a simple but effective mechanism for accessing stored data.
These techniques can be used in applications where the data is organized randomly and where
each item has a unique key associated with it.
For example, consider a table that contains computer opcode mnemonics and their associated
value as used in an assembler;
by using the opcode value as a key this table could be used to determine the mnemonic associated
with any particular value.
Such a table is an integral part of any disassembler.
In any computer, a particular entry in a table can be specified by the starting address of the entry.
Locating an item in a table implies that the starting address for that item must be determined.
One possible method that can be used to determine the address, and by far the most common method,
is to examine each item sequentially, starting with the first item, until the desired item is
located and hence the item address determined.
This approach is termed a linear search and as you can see by the the 8080 subroutine of
listing 1, it is simple to code.
The big disadvantage of a linear search is that it is costly in terms of processing time because,
on the average, at least one half of the table entries must be examined before locating the desired item.
If the table is moderately large and numerous accesses are required, then the table lookup
processing time will constitute a significant part of the total processing time.
|
Listing 1:
Typical 8080 code sequence for a linear search of a table until the first byte of the current
table entry matches the value in the accumulator.
In this listing, the HL register pair must be preset to the address of the table,
the DE register pair must be set with the number of bytes per table entry,
the B register must contain the number of entries to search (maximum 255)
and the key value sought must be loaded in A.
This is by no means the only possible 8080 linear search strategy.
|
FIND: CMP M Check for a match;
RZ If so then exit;
DAD D Advance to next table entry;
DCR B Decrement count;
JNZ FIND Continue till end;
JMP ERR Table exhausted, treat as error;
|
An alternative to the linear search involves storing the information in a sorted fashion based
upon the key.
However, even the best known algorithms for locating data in a sorted table require an average
of Log2 N tests, where N is the table size.
Therefore, a table with, let's say, 500 entries requires an average of nine tests to locate
an arbitrary item.
Although this is a considerable improvement over the linear search, which would require
an average of 250 tests to locate an item, hashing techniques require considerably fewer
tests than either method, without the added burden of sorting.
The Key
The fundamental idea behind any hashing technique is that instead of searching the table
to determine the address of a particular entry, an attempt is made to calculate the address using the key.
That is, a subroutine is written which, when given any desired key, calculates
the table location containing the item associated with that key.
If this calculation is successful, then the desired item is located with a single search.
The first step is to determine the key.
This choice will depend upon the intended use of the table.
In the opcode table mentioned earlier, the opcode value is the key since all lookup
requests are of the form:
"What is the mnemonic for the opcode X?"
On the other hand, if this same table were incorporated in an assembler or compiler,
then the mnemonic would be the key because requests are now of the form:
"What is the opcode value for mnemonic X?".
In all of our examples, we will assume that the opcode value is the key.
Direct Access Hash
Imagine that there are only a limited number of opcode values and it so happens that,
although the value is eight bits long, the opcode is uniquely determined by the rightmost three bits.
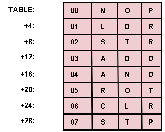
If a table, called
TABLE, is created with eight 4 byte entries, and the mnemonic
and value for each opcode is placed in the table entry whose address is found by
multiplying the rightmost three bits of the opcode by four and adding the results
to the base address of the table, then a simple subroutine can calculate
the precise location of any entry.
That subroutine, shown in
listing 2 for an 8080, simply strips
off the rightmost three bits of the key, multiplies them by four, and adds in the starting
address of the table as shown in
figure 1.
Entries are added to the table in the same manner.
Tables of this type are called
direct access and are most commonly used for conversions;
that is, converting from one character code to another, from opcode values to mnemonics, etc.
In many direct access tables the actual key is not even stored in the table since a comparison
is not necessary to determine the proper entry.
|
Listing 2:
Typical 8080 code sequence for direct hash with a table of eight entries, each entry being
four bytes in length.
In a direct hash approach, the actual data value (in this case, a number from 0 to 7)
being sought is used to determine the offset in the table directly.
Here the calculation is made according to the formula:
ADDR := BASE + 4 * (A & 7) where A is the value of the entry being sought, BASE is
the starting address of the table, and ADDR is the effective address of the table element involved.
|
FIND: LXI H,TABLE HL:=Table pointer;
ANI 7 Extract rightmost three bits;
RLC Multiply by four;
RLC
ADD L Add the table address;
MOV L,A
MVI A,0
ADC H
MOV H,A HL:=Entry address;
RET
|
|
Figure 1:
An Opcode Table Organized for Direct Access.
Note that with this particular organization the first data byte of each entry is related
to the address of the entry within the table, in a sorted sequence.
|
|
Editor's Note:
In this article, we represent several algorithms in a structured pseudo code form appropriate
to the discussion.
These algorithms are referenced by numbers in brackets, as in [n] for algorithm n.
Each algorithm should be thought of as a formal procedure, which in practice would be called
as a subroutine.
|
Open Hash
The direct access method would obviously break down if certain opcode mnemonics were associated
with values whose rightmost three bits were equal.
In this case, where direct access is infeasible, the algorithm must be slightly modified.
A subroutine is still used to calculate the address, but since it is no longer possible to
successfully calculate the location of all entries, some type of searching algorithm must
be employed to pinpoint the position of the entry, given the calculated position.
The initial predicted position of the table item is called the hash index and the
procedure which produces the hash index is called the hashing function.
For the remainder of our discussion, HASH is used to denote that subroutine
and therefore HASH(K) denotes the hash index for a particular key, K.
Before considering how the information is initially entered in a hash table, it may be useful
to examine the process used to locate an arbitrary entry in a hash accessed table.
If KEY is used to denote the key associated with the desired entry, and
TABLE, a table consisting of N entries (each of which are
B bytes long), then the algorithm to locate the entry that is associated
with KEY, using hash techniques, is as follows:
[1] 1. I,J := HASH(KEY);
2. do until (I=J-1) [worst case end test for search failure];
3. if @(TABLE + I * B) = 0 then [element not present, search failure];
4. do; call ERROR; return; end;
5. if @(TABLE + 1 * B) = KEY then
6. return [the item has been located];
7. I := I + 1;
8. if I = N then I := 0 [wrap around table space limit];
9. end;
10. call ERROR [element not present, search failure];
In this algorithm, specified in a structured pseudo code form, step 1 calculates
an initial estimate of the location of the item associated with KEY, the hash index.
This value is saved in J for the worst case end test in the
do until construct of step 2.
In steps 3 and 4, the algorithm tests for a null entry end of search criterion and
calls an ERROR routine if this is detected.
Return to the calling program follows detection and flagging of the search failure condition.
Then the algorithm tests to see if the current entry is equal to KEY at step 5;
if this condition is found, the algorithm terminates with a return operation at step 6.
Otherwise, the next index is calculated at step 7, an end around wrap condition is tested at step 8,
and the do loop is closed at step 9 with an end statement.
If the loop execution ends through the test on line 2, step 10 is reached and an error condition
is flagged before an automatic return assumed after the last line of such a procedure.
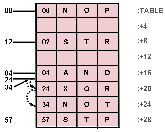
Consider again the opcode table example.
If the hash procedure is defined as
HASH(K) = REMAINDER(K/8),
then each table item shown in
figure 2 can be located by
at most three searches using algorithm
[1].
|
Figure 2:
A Hash Accessed Table.
Note that with the hash algorithm described in the text, three elements of
this table map into identical starting entries, resulting in a rehash requirement
indicated by the arrows and dotted lines.
|
Defining HASH
In choosing a hash function, you must attempt to define a general procedure,
using a minimal number of simple computations, which produces an even distribution
of hash indexes for a random selection of possible keys.
If we knew that all opcodes were even numbers, then the hashing function
HASH(K) = REMAINDER(K/8) would not be efficient, because it will produce only even numbers.
This simple example illustrates that the hashing function must be carefully selected
to suit the particular application.
It should also be noted that it is not necessary for the key to be a numeric value.
If alphanumeric or other keys are used, the hashing function should ignore the data type
and simply perform numeric or logical manipulations of the key as though it were numeric.
One of the most widely utilized, and historically the first, hashing function has already been mentioned.
If N is the size of the table (in terms of the number of entries, not the number of bytes) the hash index is the remainder of the key divided by N.
More precisely stated, HASH(K) = REMAINDER(K/N).
In a machine such as the 8080 which lacks division capability this function will be made significantly faster by restricting the length of the table to a power of two (ie: N = 2M).
If N = 2M, then the REMAINDER(K/N) also happens to be the rightmost M bits of K and a divide operation is no longer required.
The remainder is selected by a logical AND Operation.
The remaindering function will not produce well distributed hash indexes if many of the entries end with the same bit sequence.
This situation is frequently encountered when dealing with alphanumeric data.
Changing the table size to a prime number usually improves distribution, but now we are back to the unwanted divide operation for calculating the remainder.
There are two other alternatives to this problem.
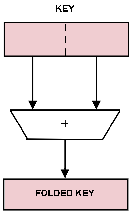
The first is a technique called
folding as diagrammed in
figure 3.
|
|
Figure 3:
Folding Keys.
When it is desired to retain the significance of all the bits in a key while compressing the total number of bits used, folding by some operation such as addition can be used.
|
This method applies the remaindering algorithm to the bit string that is obtained by adding the upper half of the internal binary representation of the key to the lower half.
This minor improvement minimizes the effect of patterns that may occur within the key.
You should be careful what improvisations are made to the folding technique.
For example, substituting a logical AND for the add sounds good, but will merely make matters worse.
If in doubt, try experimenting with various keys by examining the effects of key value in a test program to grind out hash indices.
A second method for minimizing the effect of similar bit patterns in the key, best applied to tables of size 2M, is called squaring.
This consists of selecting the center M bits of the number that is obtained by multiplying the key by itself.
Since the middle bits of the product depend upon all of the bits in the key, this method generally produces a uniform distribution of hash indices.
Since the squaring method is safest, it may appear that one should always use it.
This is certainly not the case because the purpose of hashing is to save processing time and although squaring is the most general technique, it is unfortunately the slowest since it relies on a multiply operation which the 8080 and most other small processors lack.
It is often acceptable to settle on a slightly less efficient hash function if such a function is substantially faster.
The guideline for selecting the hash function is to employ a more complex function only in those specific cases where a simple function fails to produce an adequate distribution of hash indices.
But remember, any hash function is better than a linear search.
Why?
A linear search is a hash access where
HASH(K)=0 for all values of K, therefore any distribution is better than none.
This degeneracy is evident in algorithm
[1] when the data item sought is not in the table, and the algorithm searches every location.
Multibyte Hash
Until now, we have tacitly assumed that the entire key can be contained in one byte.
This is impractical, and the hashing concept is easily extended to cover those cases where the key occupies more than a single byte.
If the key is continued in byte locations (
K1,... Kj) then a multibyte hash function,
HASHM, can be defined in terms of any of the previous hash functions as
HASHM(K,J) = HASH(K1+ ... +Kj).
That is, any of the single byte hash functions are applied to the sum, ignore carry, of the bytes in the multibyte key.
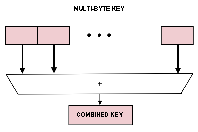
As you see in
figure 4, this is similar to the folding technique just mentioned.
Another possibility for a multibyte hash, which should be used with some degree of caution since it may not provide an even distribution, is to apply a single byte hash function to the last byte (or any other byte of your choosing) of the multibyte key.
This eliminates the time required to add the words of a multibyte key.
As usual, the programmer is faced with a time versus efficiency tradeoff.
|
|
Figure 4:
The principle of folding key elements can be extended to a multibyte key.
The multibyte hashing scheme might be employed where a key is a character string field.
|
Guidelines
In summary, the sole purpose of a hashing function is to calculate an initial table index for a linear search, given a specific key.
There is no one best algorithm and the number of algorithms available is bounded only by your imagination.
The general guidelines to follow when designing your hashing function are:
-
Keep it simple — Remember, the goal is to locate an item in the minimum amount of time.
If the perfect hash requires more time than a linear search, it is useless!
-
Insure an even distribution; beware of weird bit patterns in the key.
-
Check out the operation of the function prior to employing it as a hash function.
There is often an overwhelming urge to give it the smoke test, but hash indices are used to form memory addresses so it may be difficult to isolate bugs in the hash function after you've incorporated it into a table lookup procedure.
Save yourself some time, check the table lookup subroutines first.
Building the Table
Obviously, for the hash access algorithm to operate smoothly, the table items must have been entered into the table properly.
The relative ease with which entries can be made in a hashed table is an important advantage of hash techniques.
Remember, even though a sorted search is reasonaibly efficient for locating an entry, the entire table must be sorted before any access is allowed.
Thus, if accesses were to be intermixed with entries, the algorithm would be grossly inefficient due to the amount of resorting required.
Before any entries can be made in the hash table, the key field of the table must be initialized to some flag value which is not encountered as a possible key.
If a table entry contains this value, then it can be assumed that the entry is unoccupied.
The most common value used to designate an empty table entry is the integer zero, and assuming this to be the case, the algorithm to add an item associated with KEY, to the table of N entries (each B bytes long) is:
[2] 1. I,J := HASH(KEY);
2. do until (I=J-1) [worst case end test for search failure];
3. if @(TABLE + I * B) = 0 then
4. do;
5. [enter the item at (TABLE + I * B)];
6. return;
7. end;
8. I:=I + 1;
9. if I = N then I := 0 [wrap around table space limit];
10. end;
11. call ERROR [no roorn left in table];
Notice that the lookup algorithm
[1] and the entry algorithm
[2] are very similar in nature.
The loop control is identical, and the only difference is in the actions taken.
It is quite possible to make an automatic entry occur whenever a key is not found as indicated by a null key value found during a search.
The following algorithm combines both operations.
[3] 1. I,J := HASH(KEY);
2. do until (I=J-1) [worst case end test for search failure];
3. if @(TABLE + I * B) = KEY then
4. return [the item has been located];
5. if @(TABLE+ I * B) = 0 then
6. do;
7. [enter the item at (TABLE + I * B)];
8. return;
9. end;
10. I:=I + 1;
11. if Il = N then I :=0 [end wrap around table space limit];
12. end;
13. call ERROR [if this point is reached, table is full];
In addition to adding or locating entries, it may also be necessary to delete entries.
To delete an item, you might think that we could merely locate the item and then set the table entry to zero, thus making it available for future entries.
However, if that approach were taken, not only would the desired entry be deleted, but other entries might be made inaccessible.
The reason that other entries would be lost is that the searching terminates when an unused location is found.
As an example, setting the entry at (
TABLE + 20) in
figure 2 to zero would also make the entry at (
TABLE + 24) inaccessible.
Therefore, an alternate scheme must be used to delete entries.
The first step is to select a deleted entry flag that is distinguishable from the unused entry flag and is also not allowable as a key.
Then, whenever an entry is to be deleted this new value replaces the entry.
The new flag indicates that the entry is available for future additions to the table but does not terminate a search operation.
If 0 is used to denote an unused entry and -1 is used to denote a deleted entry, then the complete hashing algorithm is:
[4] 1. I,J:= HASH(KEY);
2. do until (I=J-1) [worst case end test for search failure];
3. if @(TABLE + I * B) = KEY then
4. do;
5. if [entry is to be deleted] then [delete the entry]
6. @(TABLE + I * B) := -1;
7. return [item has been located];
8. end;
9. if @(TABLE + I * B) = 0 then [this is a null entry so]
10. do;
11. [enter the item at (TABLE + B * I];
12. return;
13. end;
14. I := I + 1;
15. if I = N then I = 0 [end wrap around table space limit];
16. end;
17. call ERROR [if this point is reached, table is full];
This algorithm either locates an item or adds the item to the first available location.
If an item is to be deleted it is first located and then the key field of the table entry set to -1.
Collisions
A
collision occurs whenever
HASH(KEY1) = HASH(KEY2), but
KEY1 ≠
KEY2.
As discussed earlier, a good hashing function will avoid this condition, but the problems caused by collisions cannot be ignored.
Note for example that the hash index for opcodes 04, 24 and 34 in the table shown in
figure 2 is 4 and hence these entries collide.
What happens when two entries collide?
The only solution we've discussed thus far is to search the table, in a circular fashion, from the point of impact as in algorithms
[1] to
[4].
If, in general, a collision occurs, then the resulting search, good or bad, is called a
rehash.
The process mentioned above, namely, searching the table in a circular fashion from point of impact, is called a
linear rehash, and as you might expect falls into the bad category.
Other more efficient algorithms will be discussed later.
If we denote the rehashing algorithm by REHASH, then the general hashing lookup algorithm may be restated in its final form:
[5] 1. I,J := HASH(KEY);
2. K := 0;
3. do until (REHASH(I,J)=J) [worst case end test for search failure];
4. if @(TABLE + I * B) = KEY then [we have a match so]
5. do;
6. if [entry is to be deleted] then [delete the entry]
7. @(TABLE+ I * B) := -1;
8. return;
9. end;
10. if ((K=0) & [deletion or null element @(TABLE + I * B)]) then
11. K := I [save last available table entry index];
12. if @(TABLE + I * B) = 0 then [this is a null entry so]
13. do;
14. [enter the item at (TABLE + B * K), next available slot];
15. return;
16. end;
17. I := REHASH(I,J) [REHASH results in 0 ≤ I ≤ N where N is table size];
18. end;
19. call ERROR [if this point is reached, table is full];
The linear rehash that we've been using implicitly in
[4] as steps 14 and 15 is described as
REHASH(I) = (I+1)[mod N], where
(I+1)[mod N] means that if
(I+1) is greater than or equal to
N, then
N is subtracted from the value
(I+1).
This insures that the table is searched in a circular manner.
The operation
X[mod N], called
X modulo N, is used in most rehashing algorithms to limit the range.
Mathematically, it is the remainder of
X/N;
but whenever we use
X[mod N] it can be calculated as described above
(ie: subtract
N if
X is greater than or equal to
N).
Here again we have avoided the use of a divide operation to provide a more efficient function.
Improved Rehash
The problem with the simple linear rehash is that the table will not fill uniformly.
This condition is referred to as
clustering and causes an increase in the average number of tests required to locate an item in the table.
As an example, a cluster can be seen forming at
TABLE+16,
+20, and
+24 in the table shown in
figure 2.
There are a number of nonlinear algorithms which perform the rehash function without causing the clustering problems mentioned above.
Although the computer science literature abounds with such algorithms, a majority of them fall into one of three classes.
An attempt has been made to select the simplest and best from each class and present them here.
Pseudorandom Rehash
The first class of rehashing algorithms is the
pseudorandom rehash and is based upon a pseudorandom number generator.
The pseudorandom number generator used is not important, but it must be of the non-repeating variety.
That is, it must generate all possible values before any previous value is repeated.
It must also generate all of the integers in the range
0, ..., N where
N is the table size.
The following simple procedure incorporates a common random number generator and will perform the rehash function for any table of size
N = 2M.
The variable
R is internal to the rehashing function, but it must be preset to one whenever the function
HASH is initiated
(ie: step 1 of
algorithm 5).
[6] REHASH (I,J):
1. R := REMAINDER (R*5 / N*4);
2. REHASH := (R/4 + J) [mod N];
If you're seeking the most efficient implementation of this one, the REMAINDER(R*5/N*4) is just the rightmost M+2 bits of R*5 because N=2M and 4*N=22*2M=2M+2.
Furthermore, the divide operation in step 2 can be replaced by a right shift of two positions.
Finally, if you think of R*5 as R*4+R, then it's easy to see how to reduce that multiply operation to left shift and addition operations.
Let's look at the sequence generated by this rehash routine.
If our table is eight entries long and the initial hash index is, let's say, 4, then R takes on the values 1,6,7,4,5,2,3,1, so the table would be searched in the order 4(initial index),5,2,3,0,1,6,7.
How does this avoid the clustering situation?
If we chose another initial index, say, 5, then the table is searched in the order 5(initial index),6,3,4,1,2,7,0.
As you see, the entry searched after entry 5 will depend upon the initial index.
If the initial index was 4, then 2 is searched after 5;
but if the initial index was 5, then 6 follows 5.
In a linear search, 6 always follows 5.
This dependence upon the initial index is what avoids the clustering.
Quadratic Rehash
A second class of algorithms for rehashing is the
quadratic rehash and these are based upon a quadratic function.
The major drawback with most algorithms in this class is that they search only one half of the table, so two different rehashing algorithms are required.
The most efficient quadratic rehash, and one which does search the entire table, was first introduced by Colin Day [
see bibliography, reference 1].
Day's algorithm can only be applied to a table whose size is a prime number that produces a remainder of 1 when it is divided by 4 (eg: 5=4*1+1, 401=4*1+1).
At first glance, this appears to place a great many restrictions on the allowable size of the table; but don't despair, because experience will show that a number satisfying the required condition can be found very near any desired value. Be certain that you use an acceptable number or the procedure will not search all locations of the table. Like the last rehashing function an internal variable is used.
The variable,
R, must be preset to (
-N) whenever the function
HASH is called. The quadratic rehash process is (remember that the mod operation is just a conditional subtraction):
[7] REHASH(I,J):
1. R:=R + 2;
2. REHASH := (I + /R/) [mod N];
If we look at the sequence generated by this procedure, we see that R takes on the values (for a table of size 11=4*2+3) -11,-9,-7,-5,-3,-1,1,3,5,7,9,11.
Therefore, if the initial index were 4 the table would be searched in the order:
4(initial index),2,9,3,6,7,8,0,5,1,10.
One major difference between this algorithm and the random rehash is that this one calculates the next index based on the previous one.
The random rehash calculates the next index based on the initial index.
Weighted Increment Rehash
The last, and probably the simplest, method for performing the rehash is called a
weighted increment [see bibliography, reference 2].
This one is unique because it uses the hash index to calculate an increment which is in turn used to step through the table.
The table size is again restricted to a power of 2, and whenever the function
HASH is called, the variable
R is preset to
(2*J+1)[mod N], where J is the initial hash index.
The weighted increment method is:
[8] REHASH(I,J):
1. REHASH := (I+R) [mod N];
This process is very much like a linear rehash.
In fact if R were always set to 1 it would be a linear rehash, however R depends on the hash index.
If our table is eight entries long and the initial index is 5 then R=2*5+1[mod 8]=11-8=3 and the table items are searched in the order 5,0,3,6,1,4,7,2.
Since the increment is a constant for any particular hash index, we can improve the basic hash algorithm when using this rehash technique.
You will notice that all memory references are of the form (TABLE+I*B), where B is the number of bytes.
We can avoid that multiply by including it in the computation of R.
If we let R=((2*J+1)[mod N])*B, then all of the table references become (TABLE+I).
If we also initialize I to TABLE+HASH(KEY) we can make all references as just (I).
Laying Doubts to Rest
You might conceivably ask,
"What is gained by using a complex rehashing function?";
or if you're one of the more cynical observers, "Why use hashing at all?".
In an attempt to answer these questions, a simple experiment was performed.
First a table of approximately 500 entries was filled with randomly generated entries and then each entry was located in the table using the lookup technique under test.
This simple experiment provides an insight into the comparative efficiency of table lookup algorithms.
Table 1 summarizes the results of the experiment.
| % Items | Linear | Sorted | Hash Access Method With Rehash Indicated Below |
| Occupied | Search | Search | Linear | Random | Day's | Wt Inc |
10%
50%
75%
90%
|
25
125
187
225
|
5.6
7.9
8.5
8.8
|
1.1
1.5
2.5
5.5
|
1.1
1.4
2.0
2.8
|
1.1
1.4
2.0
2.7
|
1.0
1.4
1.9
2.5
|
|
|
Table 1:
Comparison of Table Access Methods.
This table gives the results of an experiment with random data to test out the various methods of access.
The tables were filled to the percentage levels indicated at the left.
A table size of 500 possible entries was used.
The access methods shown are described in text.
|
This data clearly illustrates that there is significant improvement in table lookup time when hashing is utilized.
Furthermore, when a complex rehashing algorithm is incorporated in the search procedure, the statistics are again improved.
It is worth noting again that, although the number of tests for a sorted table is not tremendously large, the approach is very inefficient if the table must be accessed before being filled with entries.
One other surprising fact about the average search length (the number of tests required) for hash accessed tables is that it does not depend upon the length of the table.
Rather, the search length depends only upon the load factor or the percentage of occupied items in the table.
This means that you can expect the average search time for a table of size 10,000 to be about the same as the search time for a table of size 500!
This is surely not the case with the linear or sorted search.
While the average linear search length skyrockets to 4,500 (for a 90% full table of size 10,000), the average hash search length remains at less than six!
Although
table 1 seems to indicate that the weighted increment is most efficient, we must be careful not to read too much into these results.
The statistics in
table 1 were obtained using randomly generated keys in the test program.
When actual keys are used the search statistics will vary somewhat because actual keys are rarely perfectly random.
For example, the search length for a weighted increment search is adversely effected by bit patterns in the key.
The best way to insure that you are using the most optimal search procedure is to repeat the experiment with a sample of actual keys.
If a finely tuned algorithm is not important, then the weighted increment is probably the better choice because it is simple and can be applied to any formal of table.
As we will see shortly, most of the algorithms work best if the table is rearranged in memory.
Application
There are a number of "tricks" which can be used to improve efficiency.
A number of them have already been mentioned.
One approach not discussed so far is table reorganization.
Throughout our discussion we have assumed that each table entry occupies more than a single byte.
If each table entry is B bytes long, then the typical memory reference is (TABLE+I*B).
It would be desirable to eliminate or at least reduce the multiply operation.
If a weighted increment rehash is used:
We already discussed how to eliminate the multiply.
Another method to eliminate a multiply is table reorganization.
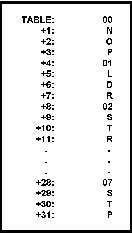
All of the tables discussed so far were horizontally organized.
This means that the items are stored as shown in
figure 5.
This is the most common table organization.
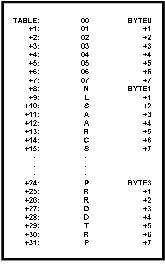
An alternative organization is a vertical organization such as in
figure 6.
|
|
Figure 5: Horizontal Organization of Tables.
In this method of organization, all the bytes of a data entry are assigned to contiguous addresses.
|
|
|
|
Figure 6: Vertical Organization of Tables.
In this method of organization, a multibyte table element is treated as "n" single byte subtables where "n " is the number of bytes in each entry.
Each of the "n" subtables has a length (in bytes) equal to the number of elements in the table.
|
|
If you have organized your table vertically then the first byte of an item is addressed by (TABLE+I) and the multiply is gone.
All of the other bytes in the item are addressed by (BYTEN+I) where BYTEN is the address of the nth byte of the first item.
Thus by organizing the data vertically we eliminate a multiply operation.
This vertical arrangement is practical from other aspects also.
Consider searching the table for all items containing a specific value in the third byte.
Since the third byte of each item is stored sequentially this search operation is simplified.
Conclusion
We have tried to show that hashing is not nearly as complicated as you might have thought.
By using these techniques perhaps you can regain a valuable slice of your microprocessor's processing load.
BIBLIOGRAPHY
-
Day, Colin A, "Full Table Quadratic Searching for Scatter Storage,"
Communications of the ACM 13,8 (August 1970), pages 481-482.
-
Luccio, F, "Weighted Increment Linear Search for Scatter Tables,"
Communications of the ACM 15,12 (December 1972), pages 1045-1047.
-
Morris, Robert, "Scatter Storage Techniques,"
Communications of the ACM 11,1 (January 1968), pages 38-44.
-
Dollhoff, Terry, "Hashing Methods for Direct Access Files,"
Auerbach Computer Programming Management, Folio 15-02-02.
GLOSSARY
|
Clustering:
Grouping of elements within a table caused by equal hash indices.
|
Linear rehash:
A method for resolving collisions.
The table is searched sequentially from the point of impact.
|
|
Collision:
Two elements with the same hash index.
|
Linear search:
Table search which examines each item starting with the first item and proceeding sequentially.
|
|
Direct access hash:
A hash algorithm which precludes collision.
That is, no two elements have identical hash indices.
|
MOD:
Remainder of one number divided by another.
That is, X MOD Y is the remainder of X/Y.
|
|
Dissassembler:
A program to translate object code to assembly language.
Inverse of an assembler.
|
Pseudorandom rehash:
A method for resolving collisions.
A nonrepeating random number generator is used to determine the next entry to be searched.
|
|
Folding:
Procedure for randomizing the hash index.
The upper and lower half of the key are added together before the index is calculated.
|
Quadratic prime:
A prime number which produces a remainder of 3 when divided by 4.
|
|
Horizontal table:
A table whose entries are stored sequentially.
That is, (entry one, byte one), (entry one, byte two), etc.
|
Quadratic rehash:
A method for resolving collisions.
A quadratic or second degree function is used to determine the next entry to be searched.
|
|
Hash index:
The initial estimate of the location of an entry within the table.
|
Rehash:
Any algorithm for resolving collisions.
|
|
Hashing:
A nonlinear algorithm for storing/retrieving data from a table.
|
Squaring:
Procedure for randomizing the hash index.
The key is multiplied by itself before the hash index is computed.
|
|
Hashing function:
The algorithm or procedure for calculating the hash index.
|
Vertical table:
A table where the bytes of each entry are stored sequentially.
That is (entry one, byte one), (entry two, byte one), etc.
FORTRAN Stores arrays in this manner.
|
|
Key:
Field within an entry that is used to locate the entry.
For example, surnames are the key field of the entries of a telephone directory.
|
Weighted increment rehash:
A method for resolving collisions.
The hash index is used to determine the next entry to be searched.
|
Im "Technical Forum" der BYTE vom Mai 1977 findet sich folgende Ergänzung:
John F Herbster
Herbster Scientific
3233 Mangum Rd, 100
Houston TX 77092
|
Improving Quadratic Rehash
"Making Hash With Tables" by Terry Domoff [BYTE, January 1977, page 18] is a good introduction to hash tables.
However, quadratic methods for collision avoidance do not have to be complicated or suffer from "half table search."
If the table length is a power of 2 and the quadratic increment is 3 as in the following simple and fast algorithm, then none of the table will be excluded from the search.
I have been using this scheme since about 1970 but have never seen it reported in the literature.
Your readers may write to me for a copy of the proof that it works.
|
|
A Quadratic Hash Table
The following algorithm assumes that the table length is a power of 2, the table words were initialized to VIRGIN, and MASK has a value equal to the table length minus 1.
- Set DEL to 0.
- Set I to hash code of KEY.
- LET I=I.AND.MASK (eg: AND I with MASK).
- IF TABLE(I)=VIRGIN then go to NOTFOUND.
(Note that TABLE(I) refers to the contents of location TABLE+1).
- If TABLE(I)=KEY then go to FOUND.
- Let DEL=(DEL+3).AND.MASK.
- If DEL=0 then go to FULL.
(Note that DEL gets back to 0 only after the whole table has been searched.)
- Let (I=I+DEL).ANO.MASK.
- Go to step 4.
On return to the user's program via the NOTFOUND, or FOUND exits, the index, I, will point to the spot for a new table entry or the found entry respectivelv.
The FULL return means the KEY was not found and that the table is full.
Note that the value VIRGIN may not equal any possible value of KEY.
|
|
Eingescanned von
Werner Cirsovius
September 2004, Erweiterung Januar 2013
© BYTE Publications Inc.


