(Im Original fehlten einige Einträge)
| Hagen Völzke |
Teil 3: Die verwendeten Algorithmen
Mit einer eingehenden Besprechung der verwendeten Algorithmen wird in diesem Teil des Artikels mit der Realisierung der Fließkommaroutinen fortgefahren.
Dabei kommen Addition, Subtraktion, Multiplikation und Division von Fließkommazahlen zur Sprache, außerdem gibt es das Listing für den Z80.
|
 |
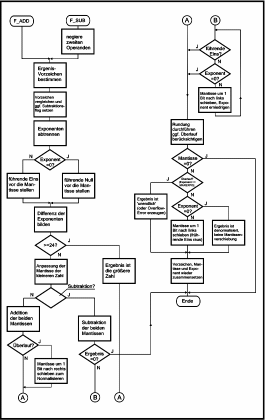
| Bild 1: Flußdiagramm zur Fließkomma-Addition/-Subtraktion
(Im Original fehlten einige Einträge) |
(MAXFLOAT+1) (größte darstellbare Fließkommazahl + 1) bzw. als -(MAXFLOAT+1) interpretiert werden können.
Werden sie vor der eigentlichen Berechnungs-Routine nicht abgefangen, so verarbeitet diese die Darstellungen von ±∞ einfach als sehr große Zahlen.
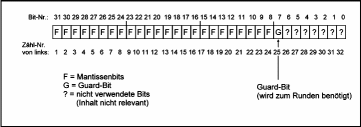 |
| Bild 2: Rundung des Zwischenergebnisses |
MAXEXPO erreicht oder überschreitet.
In diesem Fall wird als Ergebnis „unendlich" zurückgeliefert.
An dieser Stelle könnte man auch eine Überlauf-Exception oder einen Laufzeitfehler (Sprung zu einer Fehler-Routine) erzeugen.
Falls der Exponent nicht übergelaufen ist, so kann er genau Null sein.
In diesem Fall ist das Ergebnis denormalisiert, das implizite Bit ist eine Null, der Bias des Exponenten beträgt dann 126 statt 127.
Ist der Exponent ungleich Null, so wird die führende Eins aus der Mantisse ausgeschoben, da sie nicht mit abgespeichert wird (implizite Eins).
(Den unterschiedlichen Bias bei normalisierter und denormalisierter Darstellung müssen wir nicht weiter behandeln, da durch das Auslassen der Mantissenverschiebung automatisch die nötige Korrektur durchgeführt wird).
Zum Abschluß der Additionsroutine müssen nun der Exponent, das Ergebnisvorzeichen und die Mantisse wieder zusammengesetzt werden und in das im letzten Teil der Artikelserie angegebene Format einer Single-Precision-Zahl gebracht werden.
Der Bias, mit dem der Exponent einer Fließkommazahl behaftet ist, muß an keiner Stelle explizit zu- oder abgerechnet werden, da der Ergebnisexponent aus dem Exponenten der größeren Zahl gewonnen wird und damit den bereits vorhandenen Bias übernimmt.
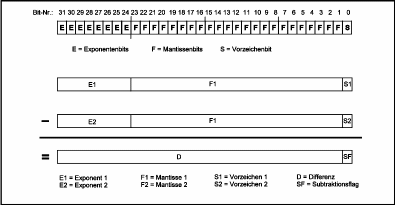 |
| Bild 3: Zur Bildung der bitweisen Differenz zweier Fließkommazahlen |
| ⌈ | wenn E1 > E2 | |
| D ≥ 0 | ⟨ | wenn El = E2 und F1 > F2 |
| ⌊ | wenn E1 = E2 und F1 = F2 und S1≥ S2 |
| — | Die Subtraktionsflag im untersten Bit (gewissermaßen die EXOR-Verknüpfung beider Vorzeichen) und |
| — | Die Aussage, welche der beiden Zahlen die größere ist. |
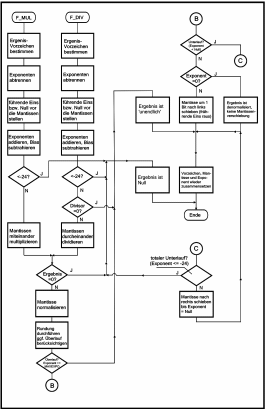 |
| Bild 4. So sehen Multiplikation und Division im Flußdiagramm aus: |
MAXEXPO erreicht hat.
Falls Überlauf eintritt, wird als Ergebnis ∞ erzeugt.
Sonst müssen wir auf Unterlauf prüfen.
Unterlauf tritt ein, wenn der Exponent kleiner als Null geworden ist (wir rechnen immer mit einem Bias-behafteten Exponenten!).
Falls der Exponent kleiner oder gleich -24 ist, so erhalten wir totalen Unterlauf und können als Ergebnis Null zurückgeben.
Sonst ist das Ergebnis denormalisiert und wir verschieben die Mantisse so oft nach rechts, bis der Exponent wieder Null wird.
(Bei jeder Verschiebung nach rechts wird zum Ausgleich der Exponent erhöht).
Diesen Vorgang nennt man denormalisieren.
Tritt kein Unterlauf ein, müssen wir prüfen, ob der Exponent genau Null ist.
Dann ist das Ergebnis ebenfalls denormalisiert.
Sonst verfahren wir wie bei der Addition: die führende Eins der Mantisse wird rausgeschoben und zum Schluß der Routine müssen nun der Exponent, das Ergebnisvorzeichen und die Mantisse wieder zusammengesetzt werden und in das Format Single-Precision-Zahl gebracht werden.
Bei der Realisierung der Fließkommaroutinen weichen wir von diesem Flußdiagramm aus Effizienzgründen leicht ab:
| — | Bei der Multiplikation wird die Mantisse nur soweit normalisiert, daß der Exponent nicht negativ wird (sonst müssen wir später wieder denormalisieren). |
| — | Bei der Division wird nicht einfach naiv dividiert, sondern die Division wird solange berechnet, bis entweder ein bereits normalisiertes Ergebnis vorliegt, oder wegen Exponentenunterlaufs abgebrochen werden muß. |
| Tabelle 1: Die schriftliche Multiplikation |
| Bild 5. Fließkomma-Arithmetik-Routinen in Z80-Assembler |
|---|
| [Source file] |
| Tabelle 2: Die schriftliche Division |
| — | von Integer nach Float |
| — | von Float nach Integer |
| — | von ASCII nach Float |
| — | von Float nach ASCII. |
Scanned by
Werner Cirsovius
September 2004
© Franzis' Verlag