Fließkomma-Arithmetik und IEEE-Spezifikationen
Teil 2: Entwurf eines Fließkommapaketes
Die IEEE-Fließkomma-Spezifikationen sind mittlerweile als internationaler Standard anerkannt.
Wie man Arithmetikroutinen schreibt, die sich an diesen Standard halten, wird beginnend mit diesem Teil der Artikelserie am Beispiel der CPUs 68000, 8086/80286 sowie des bewährten Z80 gezeigt.
|
Vorab jedoch noch einige grundlegende Feststellungen:
Bei der Diskussion der Fließkommaarithmetik sollte man nicht vergessen, daß es noch andere Möglichkeiten gibt, mit Fließkommazahlen zu rechnen als die in der IEEE-Norm vorgeschlagen.
Eine interessante Variante ist die sogenannte BCD-Arithmetik.
Bei dieser Form werden die Zahlen nicht im Binär-, sondern im Dezimalsystem gespeichert und verarbeitet.
Dies hat einige Vorteile:
| — |
die Konvertierung von Dezimal-String zur internen Darstellung und zurück ist nahezu trivial,
|
| — |
Konvertierungsfehler der Umwandlung von dezimal in binär und zurück gibt es nicht und
|
| — |
die Genauigkeit für Zehnerpotenzen nimmt stark zu.
|
Diesen Vorteilen stehen aber auch einige Nachteile entgegen:
| — |
Der Speicherplatz wird nicht so effizient genutzt wie bei Binärzahlen: Eine BCD-Ziffer belegt vier Bit, nutzt aber von den 16 möglichen Codierungen nur zehn aus, also nur 62,5 %. Zum Erreichen einer brauchbaren Genauigkeit werden also mehr Bits als bei Binärzahlen benötigt.
|
| — |
Die Rechengeschwindigkeit liegt meist wesentlich niedriger als bei binärer Darstellung, da Mikroprozessoren - wenn überhaupt - nur über sehr begrenzte Möglichkeiten zum Rechnen mit BCD-Zahlen verfügen. Außerdem steigt die Komplexität der Operationen, da z. B. Multiplikationen mit zwei durch schnelle Schiebeoperationen realisiert, Multiplikationen mit zehn hingegen nur durch konsequentes Ausmultiplizieren berechnet werden können.
|
Die IEEE-Spezifikationen wurden vor allem aus Gründen der Portabilität entwickelt.
Schließlich ist es äußerst unschön, wenn ein C-Programm auf einen anderen Rechner überspielt werden kann, dort auch fehlerfrei übersetzt wird, trotzdem aber nicht das tut, was auf der ersten Rechenanlage einwandfrei funktionierte.
Allerdings sind nicht alle Programmiersprachen unbedingt geeignet, die IEEE-Formate zu unterstützen.
Als einfaches Beispiel nehmen wir die verbreitete Programmiersprache Pascal:
In dieser Sprache gibt es nur einen Typ von Fließkommazahlen.
Der Entwickler eines Pascal-Compilers muß sich also auf einfache oder doppelte Genauigkeit festlegen, da keine Möglichkeit besteht, diese Wahl von Fall zu Fall vom Anwender treffen zu lassen.
Dabei muß man in Kauf nehmen, daß das Fließkommapaket entweder ungenau oder langsam wird.
Aus diesem Grund verwendet z.B. Turbo-Pascal ein eigenes Format, das pro Zahl sechs Byte Speicherplatz belegt.
Man hat hier einen Kompromiß zwischen Genauigkeit und Geschwindigkeit geschlossen, der beide Faktoren gleichmäßig berücksichtigt.
Gerechnet wird allerdings ähnlich wie in der IEEE-Norm, nur eben mit anderer Stellenzahl.
Dadurch entsteht natürlich gerade das Gegenteil der gewünschten Portabilität der Programme:
Selbst Daten sind nur übertragbar, wenn sie in ASCII übermittelt werden.
Die Sprache C hingegen unterstützt von vornherein die beiden Formate einfacher und doppelter Genauigkeit (float- und double-Variable).
Interne Darstellung
Um einen ersten Einblick in die Darstellung von Fließkommazahlen zu erhalten, sollten Sie eines der Beispielprogramme aus Bild 1 oder Bild 2 in Ihren Computer eingeben.
|
|
| Bild 1. Das Versuchsprogramm in Turbo-C |
|
|
|
| Bild 2. In Pascal gestaltet sich das Versuchsprogramm deutlich länger |
Das Programm liest eine Fließkommazahl von der Tastatur und gibt deren interne Darstellung als Hexadezimalzahl wieder aus.
Beide Programme erfüllen die gleiche Aufgabe;
da es sich bei der Umwandlung einer Fließkommazahl in hexadezimale Schreibweise um ein sehr maschinennahes Problem handelt, ist C hier eindeutig im Vorteil.
Bei Pascal müssen erst einmal einige Hilfsmittel bereitgestellt werden, um die hexadezimale Ausgabe zu ermöglichen.
Das ist zum einen ein varianter Record, dessen Inhalt wahlweise mit verschiedenen Datentypen angesprochen werden kann, zum anderen eine einfache Ausgaberoutine, die es ermöglicht, eine 8-Bit-Zahl (char-Variable) hexadezimal auszugeben.
Wichtig für das Pascal-Programm:
Mit der Konstanten „
zahl_der_fp_Bytes" wird das Programm an unterschiedliche Gleitkomma-Formate angepaßt.
Das ist bei C nicht nötig, da einfachgenaue sowie Long-Integer-Variable Standard sind.
Für Turbo-Pascal muß die Konstante auf 6 gesetzt werden.
Eventuell muß auch die
For-
Next-Schleife so umgebaut werden, daß sie das Array rückwärts ausliest.
Die vorliegenden Programme laufen unter Turbo-C (MS-DOS) bzw. unter OS-9-Pascal.
Dieser Pascal-Compiler verwendet - wie ersichtlich - einfache Genauigkeit.
Eine Übertragung der Programme in andere Programmiersprachen dürfte relativ leichtfallen.
Wem die hexadezimale Schreibweise nicht geläufig ist, der sollte das Programm besser so ändern, daß binäre Zahlen ausgegeben werden.
In dieser Darstellung lassen sich dann auch die einzelnen Felder (Vorzeichen, Exponent und Mantisse) leichter voneinander unterscheiden.
Wie im
ersten Teil des Artikels ausführlich beschrieben wurde, werden Fließkommazahlen nach IEEE-Norm aus Effizienzgründen im Binärsystem verarbeitet und bestehen aus drei Teilen:
Dem Exponenten e, der Mantisse m und dem Vorzeichen s (= sign).
Exponent und Mantisse sind Integerzahlen, wobei der Exponent vorzeichenbehaftet ist und mit einem Bias (= konstanter Offset) versehen wird, die Mantisse jedoch stets betragsmäßig mit getrenntem Vorzeichen abgespeichert wird (
Bild 3).
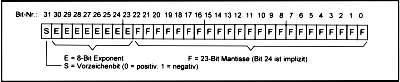 |
| Bild 3: Das Format einer Fließkommazahl in „Single-Precision", also einfacher Genauigkeit |
Die IEEE-Norm unterscheidet zwischen zwei Darstellungen:
Single-Precision und Double-Precision.
Die beiden Formate unterscheiden sich in ihrer Genauigkeit und der Rechengeschwindigkeit.
Im Rahmen dieses Artikels wollen wir sehr ausführlich beschreiben, wie die Berechnungsroutinen für Single-Precision aussehen müssen.
Ausgehend von diesen Grundroutinen lassen sich dann Routinen mit höherer Rechengenauigkeit relativ einfach ableiten.
Damit ein möglichst großes Spektrum bestehender Mikrocomputersysteme abgedeckt wird, beschreiben wir die Arithmetik-Routinen für Motorolas 68000, Intels 8086, 80286 usw. sowie für den bewährten Mikroprozessor Z80.
Da wir damit gleichzeitig ein breites Spektrum der technologischen Entwicklung der Mikroprozessortechnik abdecken, sollte es nach Studium dieses Artikels nicht schwerfallen, die Routinen auf andere Mikroprozessoren zu übertragen (z.B. 6502, 6809, MikroController und Einchip-Mikroprozessoren).
Mathematische Grundlagen
Bevor wir nun mit dem Entwurf von Berechnungsroutinen beginnen, müssen wir uns ein paar einfache mathematische Regeln zu Gemüte fuhren.
Diese betreffen das Rechnen mit Zahlen in der Exponentialform.
Betrachten wir also Zahlen im vertrauten Dezimalsystem und übertragen dann die dort gewonnenen Erkenntnisse auf das Binärsystem.
Dazu müssen wir allerdings festlegen, was wir unter einer normalisierten Zahl verstehen:
im Binärsystem ist eine Zahl normalisiert, wenn die Mantisse in der Form 1,01001... - also mit führender '1' vor dem Komma geschrieben wird.
Im Dezimalsystem heißt eine Zahl normalisiert, wenn sie in der Form d,xxxxx... geschrieben wird, also mit einer Dezimalziffer 'd' vor dem Komma, wobei d im Bereich 1...9 liegen muß;
d darf also nicht Null sein (Beispiele: 1,234; 3,14; 9,99999; 1,0; nicht: 0,5; 0,001; 120,4).
Falls nötig, muß eine Zahl durch Verschieben des Kommas (bzw. Punktes) und entsprechendes Erhöhen oder Erniedrigen des Exponenten in diese Darstellung gebracht werden.
So wird beispielsweise 0,5 * 100 zu 5,0 * 10-1.
Addition zweier Zahlen
Um zwei Exponentialzahlen addieren zu können, müssen beide den gleichen Exponenten besitzen.
Die beiden Mantissen werden dann addiert.
Beispiel:
| 4,0 * 102 |
| + 5,0 * 102 |
| = 9,0 * 102 |
Die beiden Mantissen (4,0 und 5,0) können also einfach addiert werden.
Da beide Mantissen Integerwerte sind, ist diese Operation einfach zu realisieren.
Dabei kann allerdings ein Sonderfall auftreten, wenn das Ergebnis nicht normalisiert ist:
| 4,0 * 102 |
| + 7,0 * 102 |
| = 11,0 * 102 |
In diesem Fall ergibt die Addition von 4,0 und 7,0 einen 'Überlauf':
Die Zahl 11,0 * 102 ist nicht mehr in normalisierter Darstellung.
Es ist nun ein Normalisierungsschritt notwendig, der die Darstellung 1,1 * 103 liefert.
(Kommaverschiebung nach links um eine Dezimalstelle und Erhöhung des Exponenten um Eins.)
Ein weiteres Beispiel:
| 5,0 * 103 |
| + (-3,0 * 103) |
| = 2,0 * 103 |
Hier ist der zweite Operand negativ.
Diese Operation kann man daher auch als Subtraktion interpretieren.
Man sieht, wie eng Addition und Subtraktion zusammenhängen.
In der Tat wird später nur eine einzige Routine für beide Funktionen benötigt:
Bei der Subtraktion wird nur das Vorzeichen der zweiten Zahl invertiert.
In der Additionsroutine muß eine Abfrage enthalten sein, die feststellt, ob beide Zahlen gleiche oder verschiedene Vorzeichen haben.
Bei verschiedenen Vorzeichen müssen die beiden Mantissen voneinander subtrahiert, bei gleichen Vorzeichen zueinander addiert werden.
Das Vorzeichen des Ergebnisses der Addition hängt also von den Vorzeichen und Beträgen der beiden Summanden ab.
Es empfiehlt sich, bei zwei Operanden mit verschiedenen Vorzeichen den betragsmäßig kleineren vom betragsmäßig größeren zu subtrahieren und anschließend das Vorzeichen neu zu bestimmen.
Dadurch spart man sich das Rechnen mit vorzeichenbehafteten Integerwerten.
Der Fall, daß beide Exponenten gleich sind, ist ja nur ein Spezialfall und in der Praxis eher selten.
Wie aber sieht nun die Addition von Zahlen mit verschiedenen Exponenten aus, etwa 4,0 * 102 + 5,0 * 103 = ?
Vor der Addition der beiden Zahlen 4,0 * 102 und 5,0 * 103 ist eine Exponentenanpassung notwendig.
Diese funktioniert ähnlich wie die Normalisierung.
Dabei wird der Exponent der betragsmäßig kleineren Zahl solange erhöht, bis Gleichheit beider Exponenten herrscht.
Man wählt die betragsmäßig kleinere Zahl, um den absoluten Rechenfehler möglichst klein zu halten.
Also: Der Exponent der Zahl 4,0 * 103 muß um eins erhöht werden.
Zum Ausgleich muß das Komma in der Mantisse um eine Stelle nach links wandern:
4,0 * 103 wird zu 0,4 * 103.
Diese Zahl kann nun zu der zweiten addiert werden:
| 0,4 * 103 |
| + 5,0 * 103 |
| = 5,4 * 103 |
Im Falle der Darstellung mit einfacher Genauigkeit (32 Bit) kann der Computer ungefähr 7 Dezimalstellen abspeichern, d.h. jede Zahl hat das Format d,xxxxxx * 10e (mit 1 ≤ d ≤ 9; 0 ≤ x ≤ 9; e = Exponent).
Da für die Mantisse nur sieben Stellen reserviert werden, hat es keinen Sinn, Zahlen zu addieren, deren Exponenten um mehr als sieben voneinander abweichen.
Bei der nötigen Exponentenanpassung vor der Addition wird nämlich das Komma der kleineren Zahl soweit verschoben, bis alle sieben Dezimalstellen verschwunden sind, durch die Kommaverschiebung entsteht also die Mantisse 0,000000.
Dies ist einer der markantesten Fälle, in denen die Fließkomma-Arithmetik große (relative) Rechenfehler liefert, die konzeptbedingt sind.
Vor der Exponentenanpassung ist also eine Abfrage sinnvoll, ob die Differenz der Exponenten kleiner als sieben ist.
Falls nicht, so kann sofort die betragsmäßig größere Zahl als Ergebnis der Addition zurückgeliefert werden.
Unterm Strich wird also überhaupt keine Berechnung durchgeführt.
Sie können dieses Verhalten an Ihrem Computer mit folgendem C-Programm nachprüfen:
main();
{
float a,b; /* single precision */
a = 0.0001; /* 1 * 10-4 */
b= 10000.0; /* 1 * 10++4 */
printf(„Summe: %d",a+b);
}
Als Ergebnis liefert der Rechner 10000.
Wir halten folgende Dinge fest:
-
Eine Exponentenanpassung ist notwendig, falls sich die Exponenten beider Zahlen unterscheiden.
Dabei wird das Komma der betragsmäßig kleineren Zahl um so viele Stellen nach links verschoben, wie die Differenz der Exponenten ergibt.
-
Die Exponentenanpassung ist nur sinnvoll, falls die Differenz der Exponenten die Zahl der Dezimalstellen nicht überschreitet.
Falls doch, so wird als Ergebnis die betragsmäßig größere Zahl zurückgeliefert.
-
Übertragen auf das Binärsystem bedeutet das:
Die Kommaverschiebung bei der Exponentenanpassung kann effizient durch binäre Shift-Befehle realisiert werden.
Die Exponentenanpassung ist nur sinnvoll, wenn die Zahl der Binärstellen der Mantisse dabei nicht überschritten wird (24 Stellen bei einer Single-Precision Zahl).
Die Multiplikation
Zwei Exponentialzahlen werden miteinander multipliziert, indem die beiden Mantissen miteinander multipliziert werden und die beiden Exponenten zueinander addiert werden.
Beispiele:
4,0 * 102
* 2,0 * 103
= 6,0 * 105
4,0 * 102
* 5,0 * 10-2
= 20,0 * 100
= 2,0 * 101
9,9 * 100
* 9,9 * 101
= 98,01 * 101
= 9,801 * 102
|
3,4 * 102
*-2,0 * 102
=-6,8 * 104
4,1 * 10-5
* 1,0 * 106
= 4,1 * 101
|
Man sieht, daß bei der Multiplikation auch sehr unterschiedliche Exponenten verarbeitet werden können (letztes Beispiel).
Die Multiplikation gestaltet sich etwas einfacher als die Addition, da keine Exponentenanpassung notwendig ist.
Auf vielen Computern läuft die Multiplikation daher genauso schnell ab wie die Addition von Fließkommazahlen.
Allerdings wird für die Multiplikation der Mantissen ein Integer-Multiplikations-Befehl benötigt.
Ist dieser nicht im Befehlssatz des verwendeten Mikroprozessors enthalten, so verringert das natürlich die Rechengeschwindigkeit der Arithmetik spürbar.
Das Vorzeichen des Ergebnisses richtet sich nach den Vorzeichen der beiden Faktoren:
Haben beide das gleiche Vorzeichen, so ist das Ergebnis positiv, haben beide verschiedene Vorzeichen, so ist das Ergebnis negativ.
Wir können für die Multiplikation folgendes festhalten:
Eine Exponentenanpassung ist nicht notwendig, die Realisierung im Binärsystem ist verhältnismäßig einfach, ausschlaggebend für die Rechengeschwindigkeit ist vor allem die Zeit, die für die Berechnung des Mantissenproduktes benötigt wird.
Überlauf und Fehlerbehandlung
Bislang wurde noch keine Fehlerbehandlung besprochen.
Sowohl bei der Addition als auch bei der Multiplikation können an verschiedenen Stellen Fehler auftreten:
-
Das Ergebnis ist größer als die größte darstellbare Zahl.
Man spricht dann vom Überlauf.
Eventuell kann der Überlauf auch erst beim Normalisieren der Mantisse auftreten!
-
Das Ergebnis ist kleiner als die kleinste darstellbare Zahl.
Man spricht in diesem Fall vom Unterlauf.
Falls denormalisierte Zahlen unterstützt werden, so erhalten wir zunächst einen graduellen Unterlauf (das Ergebnis ist dann eine denormalisierte Zahl) und bei weiterer Verringerung des Ergebnisses den totalen Unterlauf.
Sowohl bei Überlauf als auch bei Unterlauf hat man mehrere Möglichkeiten zur Fehlerbehandlung:
-
Abliefern eines definierten Ergebnisses (Größte darstellbare Zahl bei Überlauf, Null bei Unterlauf)
-
Abliefern einer NaN (= Not-a-Number).
-
Abbruch über einen Trap-Handler (signalling NaN).
-
Einer oder mehrere Eingabeparameter sind bereits NaNs oder unendlich.
Vor die eigentliche Rechenroutine muß also eine Abfrage gestellt werden, die NaNs erkennt und ein entsprechend definiertes Ergebnis abliefert (meistens wieder NaN).
Implizite Bits und Rundung
Im IEEE-Format wird ja von der Mantisse die führende Eins nicht abgespeichert, sondern lediglich 'in Gedanken' gemerkt.
Vor der eigentlichen Berechnung muß diese implizite Eins wieder hinzugefügt werden.
Bei einer denormalisierten Zahl handelt es sich nicht um eine implizite Eins, sondern um eine implizite Null.
Schon hier sieht man, daß zum eigentlichen Berechnen auf jeden Fall eine um ein Bit höhere Stellenzahl benötigt wird als zur Darstellung und Abspeicherung einer Fließkommazahl.
Im Falle der Darstellung einfacher Genauigkeit mit 24-Bit-Mantisse wird man daher in der Praxis mit 32-Bit-Zahlen arbeiten, im Falle doppelter Genauigkeit (52-Bit-Mantisse) mit 64-Bit-Integer-Werten.
Die höhere Stellenzahl ist auch nötig, um Zwischenergebnisse während der Berechnung mit größerer Genauigkeit darstellen zu können.
Nach der eigentlichen Berechnung der Summe bzw. des Produktes zweier Fließkommazahlen muß noch die vorgeschriebene Rundung durchgeführt werden.
Je nach dem Aufwand, den man treiben möchte, kann man zwischen verschiedenen Rundungsarten der IEEE-Spezifikation unterscheiden.
Für die Praxis ist allerdings die vollständige Implementierung der IEEE-Vorschriften ziemlich aufwendig.
In vielen Applikationen - etwa bei Steuerungsaufgaben - ist stets gesichert, daß nur normalisierte Zahlen als Eingaben vorliegen.
Für die Rundung wird fast immer 'round-to-nearest' gewählt, d.h. das 'natürliche' Auf- und Abrunden zur nächsten Zahl.
Da eine Fehlerbehandlung immer Probleme bereitet, verzichtet man gerne darauf und gibt im Falle von Über- und Unterlauf die größte darstellbare Zahl bzw. Null als Ergebnis zurück.
In einem guten Programm sollten ohnehin Sicherheitsabfragen vorhanden sein, die das Überschreiten von Grenzwerten bereits frühzeitig erkennen.
Für Steuerrungs- und Regelaufgaben ist dies ohnehin unerläßlich.
Bei der Implementation der Arithmetikroutinen bleibt uns also viel Spielraum, einfache Versionen oder den vollständigen Standard zu wählen.
Die Kernroutinen bleiben dabei nahezu identisch, lediglich die Zahl der Sonderfälle und entsprechende Maßnahmen blähen die Programme beim vollständigen Standard auf.
Subtraktion und Division
Die Subtraktion ist ein Spezialfall der Addition, daher muß kein eigener Algorithmus entworfen werden:
Man invertiert das Vorzeichen des Subtrahenden und springt dann in die Additionsroutine.
Die Division hingegen gestaltet sich etwas schwieriger:
Zuerst muß hier geprüft werden, ob der Divisor Null ist - dann muß nämlich eine Fehlermeldung zurückgeliefert werden.
Im Falle einer einfachen Implementation könnte man alternativ plus oder minus unendlich als Ergebnis erzeugen.
Während bei der Multiplikation die Exponenten beider Zahlen addiert werden, muß man bei der Division die Exponenten beider Zahlen voneinander abziehen.
Analog verfährt man mit den Mantissen:
Statt sie zu multiplizieren, werden sie durcheinander dividiert.
Diese Division muß leider meistens „zu Fuß" realisiert werden, da man sich schlecht auf vorhandene Integer-Divisionsbefehle abstützen kann.
Wir zeigen im nächsten Teil dieser Serie effiziente Verfahren für Divisions- und Multiplikationsroutinen, die man aus den schriftlichen Verfahren, wie sie in der Schule gelehrt werden, ableiten kann.
Auch zur Division wieder ein paar Beispiele:
4,0 * 102
/ 2,0 * 103
= 2,0 * 10-1
9,3 * 107
/ 3,1 * 106
= 3,0 * 101
|
6,0 * 101
/ 6,0 * 10-1
= 1,0 * 102
2,0 * 104
/ 4,0 * 102
= 0,5 * 102
= 5,0 * 101
|
Betragsfunktion, Vergleich, NaNs und höhere Funktionen
Die Funktion '
abs()' zur Bildung des Absolutbetrages ist trivial:
Es muß lediglich das Vorzeichenbit der zu behandelnden Zahl auf Null (positiv) gesetzt werden.
Genauso einfach läßt sich die Funktion '
neg()' realisieren, die eine Zahl negiert.
Dazu muß lediglich das Vorzeichenbit der zu negierenden Zahl invertiert werden.
Für diese beiden Funktionen werden wir daher keine Routinen entwerfen.
Sie können am einfachsten durch Makros realisiert werden, da für das Ändern eines einzigen Bits meistens nur ein einziger CPU-Befehl benötigt wird.
Ein Unterprogrammaufruf mit seiner Parameterübergabe sowie Hin- und Rücksprung, erfordert dagegen ein Vielfaches an Programmcode und Zeit.
Zum Vergleich zweier Fließkommazahlen werden die Zahlen mit '
f_sub' voneinander subtrahiert, anschließend wird das Ergebnis der Subtraktion mit Null verglichen.
Auch hierfür benötigen wir keine eigene Routine, da wir für den Vergleich normale Integerbefehle verwenden können.
Dies ist zulässig, da die Fließkommazahlen beim Vergleich mit Null gewissermaßen 'kompatibel' zu Integerzahlen sind.
Einziges Problemkind ist die negative Null, die bei einem Vergleich mit positiver Null 'Gleichheit' erzeugen soll.
Da unsere Routinen jedoch nie eine negative Null erzeugen, ist es zulässig, nach einer Subtraktion einen Integer-Test auf 'Null', 'größer-Null' und 'kleiner-Null' durchzuführen.
Spätere Beispiele für die Anwendung des Fließkommapaketes werden das noch verdeutlichen.
Für die Behandlung von NaNs gilt ein für alle Funktionen einheitliches Verfahren:
-
non-signalling NaNs (lösen keine Exception aus):
falls einer der beiden Operanden eine NaN ist, so wird diese NaN als Ergebnis zurückgegeben.
Falls beide Operanden NaNs sind, so wird die NaN von Operand 1 zurückgegeben.
-
signalling NaNs (lösen Exception aus):
falls einer der beiden Operanden eine NaN ist, so wird versucht, eine 'signalling-NaN-Exception' auszulösen.
Ist diese Exception gesperrt, so wird die NaN in eine non-signalling NaN konvertiert und es wird bei 1. fortgefahren.
Der IEEE-Vorschlag sieht vor, daß die Erzeugung von Exceptions wahlweise gesperrt oder freigegeben werden kann.
Das Erzeugen einer Exception hat eigentlich nur Sinn, wenn damit eine Umgebung - wie z.B. ein Betriebssystem oder eine Laufzeitbibliothek - aufgerufen werden kann.
Bei kleinen Computersystemen (z.B. für Steuerungsaufgaben) wählt man lieber die direkte Abfrage des Ergebnisses durch entsprechene Programmbefehle.
Für jede arithmetische Funktion ist in
Tabelle 1 eine Verknüpfungstafel angegeben.
| Tabelle 1: Verknüpfungstafeln für die einzelnen Operationen |
Aus dieser Tafel geht hervor, wie das Ergebnis in Abhängigkeit der beiden Operanden ermittelt wird.
Unter höheren Funktionen sollen alle Funktionen verstanden werden, die auf den Grundfunktionen aufbauen und in der Regel durch iterative Verfahren berechnet werden.
Beispiele hierfür sind Sinus und Cosinus, Logarithmus, Exponential- und Wurzelfunktion.
Es gibt verschiedene Möglichkeiten zur Berechnung dieser Funktionen, am gebräuchlichsten sind Polynomberechnungen.
Aber auch die Konvertierungsfunktionen zur Umwandlung einer Zeichenkette in eine Fließkommazahl und umgekehrt sind schon höhere Funktionen, da sie aus einer Vielzahl von Grundfunktionen bestehen.
Sie lassen sich daher am besten in einer Hochsprache formulieren.
Das Fließkommapaket
Zunächst wollen wir uns jedoch mit den Grundrechenarten beschäftigen.
Anhand von Flußdiagrammen werden wir nun die prinzipielle Arbeitsweise der Fließkommaroutinen erläutern und anschließend in Assemblersprache realisieren.
Die Routinen wurden vom Leistungsumfang gegenüber dem vollen IEEE-Vorschlag etwas beschränkt, was am besten mit den verfolgten Zielen bei der Entwicklung des Fließkommapaketes begründet werden kann.
Das Fließkommapaket wurde entworfen
- als Musterlösung zum Verständnis der Thematik
- als Vorlage zum Schreiben eigener Fließkommaroutinen
- zum konkreten Einsatz der abgedruckten Routinen - auch ohne vollständiges Verständnis - auf kleinen Computersystemen, Einplatinencomputern und Mikrocontrollern, also überall dort, wo nicht auf vorhandene Fließkommabibliotheken zurückgegriffen werden kann.
Aufgenommen wurden jeweils ein kleines Rahmenprogramm, das die einzelnen Fließkommaroutinen mit verschiedenen Parametern aufruft sowie die eigentlichen Arithmetikroutinen.
Die Programme haben die gleiche Funktion und liefern bei Ausführung das Testergebnis aus
Bild 4.
40400000
00700000
7F800000 | drei Additionen |
35BFFFFF
00400000
7F7FFFFF | drei Multiplikitiontn |
7F800000
406DB6DB
15400001 | drei Divisionen |
|
|
| Bild 4: Ob 68000, 8086 oder Z80: Die Testausgabe der Fließkommapakete sieht in jedem Fall gleich aus |
Die abgebildeten Programme wurden auf folgenden Betriebssystemen und Assemblern entwickelt und getestet:
Das Programm für die CPU 68000 unter OS-9/68K mit dem 'R68' (Microware) (
Bild 5) und das 8086-Programm unter MS-DOS mit 'MASM 5.0' (Microsoft) (
Bild 6).
Ein äquivalentes Programm für den 8-Bit-Prozessor Z80 unter CP/M-80 (für den Assembler 'M80' von Microsoft) folgt im nächsten Heft.
Die Routinen können noch an einigen Stellen optimiert werden (was vor allem bei Sonderfällen höhere Rechengeschwindigkeit bringt), bieten aber auch so schon eine gute bis sehr gute Rechengeschwindigkeit bei voller Kompatibilität zur IEEE-Norm.
Die Funktionen des Fließkommapaketes sind dabei folgendermaßen begrenzt bzw. definiert:
- Die Verarbeitung von NaNs muß - falls gewünscht - vom Programmierer selbst vor die eigentlichen Berechnungsroutinen gestellt werden (die Abfragen müssen entsprechend den Verknüpfungstafeln aus Tabelle 1 erfolgen).
- Über- und Unterlauf erzeugen 'unendlich' (bzw. 'minus-unendlich') und Null (konform mit IEEE).
- Division durch Null erzeugt 'plus-/minus-unendlich' (konform mit IEEE).
- Exceptions werden nicht unterstützt.
- Rundung erfolgt stets nach 'round-to-nearest', d.h. Auf- bzw. Abrunden zur nächsten Zahl.
Andere Rundungsarten werden nicht unterstützt.
Daraus folgen weitere Punkte:
-
Keine Routine erzeugt als Ergebnis 'minus-Null'.
Dies ist konform zum IEEE-Standard, der die Erzeugung der negativen Null nur in der Rundungsart 'gerichtet zur nächsten kleineren Zahl' vorsieht (directed-rounding-mode nach minus-unendlich).
Wir benutzen allerdings stets round-to-nearest und erzeugen daher nie 'minus-Null'.
-
Minus-Null wird jedoch als Eingabe akzeptiert und genauso wie Plus-Null bewertet (ist standardtreu).
-
Denormalisierte Zahlen werden voll unterstützt.
Notation
Wenn ein 68000- oder VAX-Programmierer die Anweisung 'FSUB a,b' liest, so versteht er darunter die Differenz 'b-a', ein Z80-bzw. 8086-Programmierer jedoch sieht die umgekehrte Differenz 'a-b'.
Um solche Verwechslungen auszuschließen, wird hiermit eine Notation festgelegt, die sich an die in C übliche funktionale Schreibweise anlehnt:
f_sub(a,b) steht für die Subtraktion 'a-b'.
Wir nennen 'a' den ersten und 'b' den zweiten Operanden.
Die Operanden werden in umgekehrter Reihenfolge ihres Auftretens auf dem Stack abgelegt.
Top of Stack liegt also jeweils der erste Operand, tiefer auf dem Stack liegen weitere Operanden.
Bei der Version für die CPU 68000 werden beide Parameter in Registern übergeben.
Die Unterprogramme erhalten die Namen f_add, f_sub, f_mul und f_div, um nicht mit Mnemonics der Assemblersprache in Schwierigkeiten zu kommen (etwa bei Verwendung von 'fadd' usw.).
Noch ein paar Worte zur Terminologie:
In den einführenden Beispielen wurde das Normalisieren immer als Verschiebung des Kommas dargestellt.
In den Routinen sprechen wir nun von der Verschiebung der Mantisse.
Bild 7 soll nun die unterschiedliche Sprechweise verdeutlichen.
 |
| Bild 7: Äquivalenz von Komma- und Mantissenverschiebung |
Wir denken uns während der Rechenoperationen das Komma immer fest hinter dem führenden Bit der Mantisse.
Eine Kommaverschiebung nach links um eine bestimmte Stellenzahl ist daher gleichwertig mit der Verschiebung der Mantisse nach rechts um die gleiche Stellenzahl.
Bei der Addition und Subtraktion werden die Mantissen stets linksbündig innerhalb des 32-Bit-Registers bzw. -Speicherplatzes gehalten.
Im
nächsten Teil des Beitrages werden die in den Programmen enthaltenen Grundrechenarten Addition, Subtraktion, Division und Multiplikation sowie Details der Assemblerlistings besprochen.
Dort finden Sie dann auch das Z80-Programm.
Eingescanned von
Werner Cirsovius
September 2004
© Franzis' Verlag


