|
Im Magazin „MC" wurde im Juni 1987 der folgende Artikel abgedruckt.
|
Grundlegender Artikel zum Zeichnen einer Geraden
|
In der hier vorgestellten Form sind die Beispielprogramme so nicht unter CP/M lauffähig
Hier ein Projekt, wo der Algorithmus eingesetzt wird
|
|
Schneller Drawline-Algorithmus
Noch immer gibt es Computer, die standardmäßig nicht über die wichtigsten Grafikbefehle verfügen oder bei denen man feststellt, daß zwar Grafiklösungen vorhanden sind, deren Geschwindigkeitsverhalten aber nicht optimal ist.
Beispielhaft sei hier Turbo-Pascal erwähnt, für das, sofern es nicht auf einem IBM-PC oder Kompatiblen eingesetzt wird, keine Grafikbefehle zur Verfügung stehen.
Es bleibt einem nichts anderes übrig, als sich entweder ein entsprechendes Grafik-Paket zu besorgen oder aber selbst zur Tastatur zu greifen.
Am Anfang einer Grafikbibliothek stehen meist Befehle wie Einschalten des Grafikbildschirms, Löschen der Grafikseite, Setzen eines Punktes und Zeichnen einer Linie.
Das Löschen ist zumindest bei einem memory-mapped Grafikspeicher unproblematisch
(Man lösche einfach den entsprechenden Speicherbereich).
Das Aktivieren des Grafikbildschirmes und das Setzen eines Punktes hingegen sind rechnerspezifisch; eine allgemeine Lösung läßt sich nicht angeben.
Ist jedoch ein Weg zum Setzen eines Punktes gefunden, so läßt sich allgemein ein „Drawline-Algorithmus" angeben, da man das Zeichnen einer Linie als Setzen von Punkten nach einem bestimmten Verfahren verstehen kann.
Doch wie so oft führen auch hier viele Wege zum Ziel, gefunden werden sollte jedoch der beste oder aber zumindest ein guter Weg.
Vorgestellt werden soll daher ein aus dem sogenannten „
Bresenham-Algorithmus" abgeleiteter Algorithmus zum Zeichnen einer Linie (zusammengesetzt aus einzelnen Punkten), wobei wir jedoch zum Verständnis auch die Herleitung dieses Algorithmus und eine Geschwindigkeitsoptimierung nicht vernachlässigen wollen.
Einige werden jetzt sagen, „Das interessiert doch gar nicht, Hauptsache es läuft", viele andere, und ich zähle mich selbst hinzu, finden diese Einstellung unbefriedigend.
Bei Benutzung eines solchen Algorithmus möchte man doch auch etwas über den Hintergrund erfahren und deshalb gehen wir hier etwas ausführlicher darauf ein.
Die Herleitung des Algorithmus gliedert sich in vier Punkte:
- Mathematische Formulierung einer Ursprungsgeraden
- Übertragung auf Programmierebene
- Geschwindigkeitsoptimierung
- Verallgemeinerung für beliebige Geraden
Aufgabe des endgültigen Algorithmus wird es sein, zwei beliebige durch ihre Koordinaten gegebene Punkte P1(x1,y1) und P2(x2,y2) durch eine gerade Linie verbinden.
Mathematische Formulierung einer Ursprungsgeraden
Zur Bestimmung der Funktion einer Ursprungsgeraden wie in
Bild 1 ist lediglich deren Steigung m zu ermitteln.
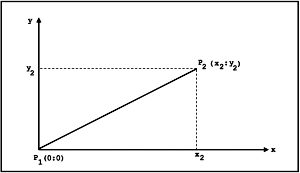 |
| Bild 1. Die Funktion einer Geraden wird durch ihre Steigung bestimmt |
Da uns die Koordinaten von P2 (x2, y2) bekannt sind, gilt:
m = y2/x2 und damit die Geradengleichung [1]
f(x) = (y2/x2) * x
Übertragung auf Programmierebene
Bevor wir zur eigentlichen Entwicklung schreiten, treffen wir noch eine Einschränkung, und zwar:
y2 < = x2, d.h. m < = 1
Warum diese Einschränkung?
Hierzu betrachten wir die zu zeichnende Linie genauer:
Der Bildschirm ist in eine Punktmatrix, wie in
Bild 2 gezeigt, eingeteilt.
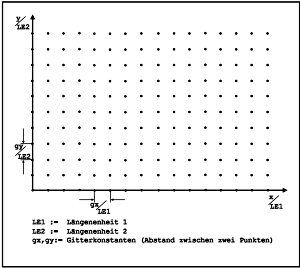 |
| Bild 2. Die Punktmatrix eines Bildschirms |
Wollen wir eine Linie zeichnen, so suchen wir die Punkte, die möglichst nahe an der Geraden liegen und setzen diese.
Die Genauigkeit wird also maßgeblich durch den Abstand zwischen zwei möglichen Punkten, den Gitterabstand, beeinflußt.
Betrachten wir diese Punktmatrix als Koordinatensystem mit den Einheiten gx (Gitterabstand in x-Richtung) und gy (Gitterabstand in y-Richtung):
Wir zeichnen eine Linie, indem wir zu jedem Punkt x (x1 < = x < = x2, x ist ein Vielfaches von gx) den Punkt y suchen, der am nächsten an der Linie liegt.
Die Darstellung in
Bild 3 verdeutlicht dieses Verfahren (ein Kreuz bedeutet: Punkt gesetzt).
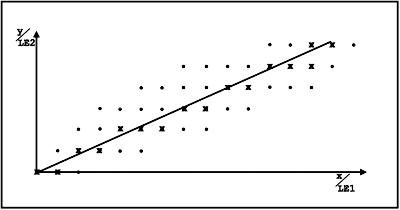 |
| Bild 3. Eine Linie wird gezeichnet |
Haben wir nun obige Einschränkung gemacht, so kann dies in einer Schleife durch Inkrementieren (≡ + 1, da gx/LE1 = 1) von x erreicht werden, bis x schließlich x2 erreicht.
Was würde passieren, wenn wir diese Einschränkung nicht gemacht hätten?
Verdeutlicht wird dies in
Bild 4.
 |
| Bild 4. So würde eine Linie ohne die im Artikel beschriebenen Einschränkungen gezeichnet |
Die Anzahl der Punkte zur Approximation einer Linie wäre unzureichend
(Während in
Bild 3 zur Approximation einer Linie 16 Punkte gesetzt werden, sind dies in
Bild 4 für eine in etwa gleich lange Linie nur 7 Punkte; als Extremfall stelle man sich eine fast senkrechte Linie vor).
Unter den angegebenen Einschränkungen läßt sich eine Linie demnach wie folgt approximieren:
a) Man berechne für alle x (x1 < = x < = x2, xεQ) f(x), also den dazugehörigen Funktionswert auf der Geraden
(eigentlich handelt es sich natürlich nur um eine Strecke)
b) Man berechne durch Rundung den dem berechneten Wert am nächsten gelegenen Punkt
(Rundung auf ganze Zahlen, da x, yεQ).
Also gilt
[2]:
Y: = ROUND (x * y2/x2),
x1 < = x < = x2, xεQ.
Prinzipiell liefert dieser Algorithmus natürlich (unter den angesprochenen Restriktionen) ein richtiges Ergebnis.
Die Ausführungsgeschwindigkeit wird jedoch durch REAL-Multiplikation und REAL-Division negativ beeinflußt.
Geschwindigkeitsoptimierung
Will man den so gewonnenen Algorithmus optimieren, muß man zweifellos an dem Rundungsbefehl ansetzen.
Das Ziel ist dabei, die Berechnung auf INTEGER-Anweisungen zurückzuführen und möglichst nur die Grundrechenarten + und - zu verwenden.
Ist dieses Ziel erreicht, wäre auch eine hardwaremäßige Lösung denkbar.
Schritt für Schritt wollen wir den oben gefundenen Algorithmus
[2] optimieren:
Y: = ROUND (x * y2/x2)
Gemäß
[2] muß gelten, daß der zu berechnende y-Wert gleich oder um eins größer ist als der vorherige.
Bei Einhaltung der gefundenen Regeln ergibt sich das in
Bild 5 wiedergegebene Programm.
|
|
|
Bild 5. Der Algorithmus wird optimiert
|
|---|
Eine hohe Verarbeitungsgeschwindigkeit ergibt sich aus drei Gründen:
- Die Anzahl der Operationen in der Schleife ist minimal.
- Es kann ausschließlich mit INTEGER-Variablen gearbeitet werden.
- Es treten (abgesehen von der Multiplikation mit 2, die sich durch ein „shift left" realisieren läßt) nur Addition und Subtraktion (keine zeitraubenden Punktrechnungen) auf.
Verallgemeinerung des Algorithmus
Um einen allgemeingültigen „Drawline-Algorithmus" für beliebige Geraden zu erhalten, versucht man alle möglichen Fälle des Linienverlaufes auf den besprochenen „Original-"Bresenham-Algorithmus zurückzuführen.
Speziell müssen der beliebige Anfangspunkt sowie alle möglichen Steigungen der Geraden berücksichtigt werden.
a) Berücksichtigung des Anfangspunktes
Benutzt man einen beliebigen Anfangspunkt, so ergeben sich zwei Änderungen:
- Die Steigung der Geraden ist nicht mehr m = y2/x2.
Statt dessen wird sie mit m = (y2-y1)/(x2-x1) berechnet.
In diesem Sinne werden die beiden Variablen dx und dy definiert mit
dx: = (x2-x1)
dy: = (y2-y1)
Entsprechend sind in dem Algorithmus aus
Bild 5 x2 durch dx und y2 durch dy zu ersetzen.
- Die Gerade soll erst ab dem Punkt P1 (x1,y1) gezeichnet werden.
Dazu sind die Variablen (x,y), die den jeweils zu setzten Punkt bezeichnen, auf diesen Anfangswert zu setzen.
Von diesem Punkt aus wird die Gerade dann, wie in
Bild 5 gezeigt, gezeichnet.
b) Berücksichtigung der Steigung der Geraden
Mit Hilfe geeigneter Umrechnungen versucht man die möglichen Lagen der Gerade auf den Algorithmus aus
Bild 5 zurückzuführen.
Insgesamt sind vier Fälle zu unterscheiden:
- Die Gerade genügt den Restriktionen aus
Bild 5, d.h. der „Original-Algorithmus" kann angewandt werden.
- Die Steigung der Geraden ist größer als m = 1.
In diesem Fall muß eine Spiegelung an der Winkelhalbierenden erfolgen, d.h.
(x,y) → (y,x)
Der Algorithmus aus
Bild 5 kann somit angewandt werden.
- Um den Originalalgorithmus verwenden zu können, muß die Gerade an der y-Achse gespiegelt werden, d.h. die Schleife aus
Bild 5 muß in umgekehrter Richtung durchlaufen werden, (x → -x)
- Die Gerade muß an der y-Achse gespiegelt werden, um den Originalalgorithmus anzuwenden (y → -y).
U.U. muß die Schleife in y-Richtung in entgegengesetzter Richtung durchlaufen werden (falls m ≤ -1).
Allgemein wird also bei Spiegelung an einer der Achsen in Abhängigkeit von der Steigung die Durchlaufrichtung der Schleife geändert, wobei gleichzeitig die Reihenfolge der Eingabe der Endpunkte P1 und P2 berücksichtigt wird.
Der in dieser Form verallgemeinerte Algorithmus ist in
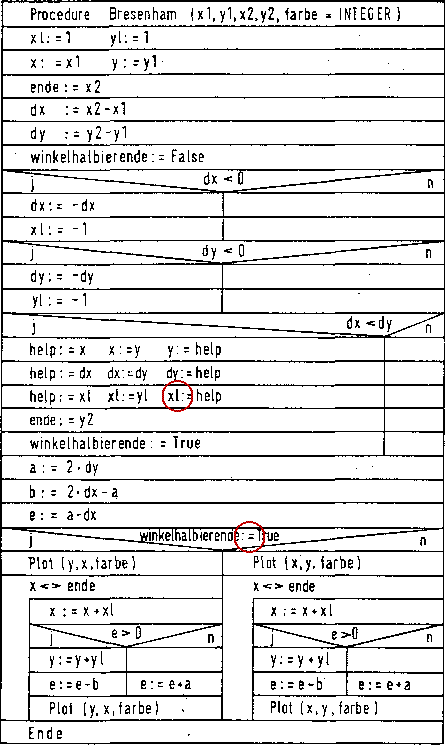
Bild 6 in einer Pascal-Prozedur entwickelt worden (das Struktogramm zeigt
Bild 7).
|
|
| [Listing] |
|
Bild 6. Die vollständige Linie-Prozedur 1
|
|---|

|
|
|
Bild 7. Der Programmablauf im Nassi-Shneidermann-Diagramm.
[Rechts das Original mit Fehlern]
|
|---|
Zur Prüfung des Zeitverhaltens ist dieser Algorithmus auf einem Commodore PC10 unter Turbo-Pascal getestet worden.
Mit Hilfe der den
Bildern 8 und
9 zu entnehmenden Programme wurde der Bresenham-Algorithmus mit dem unter Turbo-Pascal vorhandenen DRAW-Algorithmus verglichen.
Das Ausfüllen des Bildschirms mit senkrechten Linien dauerte mit dem implementierten Algorithmus ca. 27 Sekunden und mit dem in Pascal programmierten Bresenham-Algorithmus ca. 28 Sekunden.
Für einen in Pascal programmierten Algorithmus eine ansehnliche Zeit.
|
|
| [Listing] |
|
Bild 8. Der Bildschirm wird mit dem DRAW-Befehl gefüllt
|
|---|
|
|
| [Listing] |
|
Bild 9. Mit der Prozedur Linie wird der Bildschirm gefüllt
|
|---|
| 1. |
Dieses Modul diente als Grundlage zum Erstellen eines Assembler-Moduls.
Dazu habe ich ein kleines TURBO-Pascal kompiliert und anschließend disassembliert.
Ein Einblick in den Arbeitsablauf findet sich hier.
 |
Eingescanned von
Werner Cirsovius
März 2003, Ergänzung Oktober 2012
© Franzis' Verlag

