|
3. Teil
Suchen ist eine der elementaren Aufgaben von Rechenmaschinen.
Wie im täglichen Leben zeigt sich dabei, daß geordnete Daten leichter zu durchsuchen sind, als ungeordnete.
Ein Optimum an Suchgeschwindigkeit wird dann erreicht, wenn aus dem Suchschlüssel gleich der Speicherort der Information errechnet werden kann.
Mit Technik der Streuspeicherung bemüht man sich, dieses Optimum zu erreichen.
Allerdings wird dann die Eingabe der Daten durch den komplizierteren Aufbau der Datenlisten belastet.
|
Suche in geordneten Daten
Das Verfahren LINSEARCH benötigt im ungünstigsten Fall N Suchschritte.
Wenn dagegen die Daten in sortierter Folge vorliegen, läßt sich die Zahl der Suchschritte auf LOG2N reduzieren.
Dazu wird der Algorithmus der sukzessiven Halbierung verwendet, den Sie beim Sortieren durch binäres Einfügen kennengelernt haben.
Bei dem folgenden Programm ergeben sich für den Fall, das STATUS = ENDOFDATA ist die beiden „Nachbarn" D[POS-1] und D[POS].
Wenn also die Elemente des Feldes ab POS um ein Element weitergeschoben werden, läßt sich an dieser Stelle ein neues Element einfügen und so durch stufenweises Einsortieren eine Liste aufbauen.
Ein wesentlich effizienteres Verfahren zur Listenerzeugung finden Sie jedoch im folgenden Abschnitt (siehe die Programme in Bild 19 und Bild 20).
PROCEDURE BINARYSEARCH (VAR D :DATA; GESUCHT : INTEGER;
VAR STAT : STATUS; VAR POS : INTEGER);
(* DURCHSUCHEN DES FELDES D NACH DEM SCHLUESSEL 'GESUCHT'.
DIE VARIABLE 'STAT' GIBT AN, OB DIE SUCHE ERFOLGREICH
WAR (STAT = FOUND) ODER NICHT (STAT = ENDOFDATA).
DIE VARIABLE POS GIBT IM ERFOLGSFALL DIE POSITION DES
GEFUNDENEN ELEMENTES (D[POS]) AN.
GLOBALE KONSTANTE : N FELDLAENGE
GLOBALE TYPEN :
ITEM = RECORD KEY : INTEGER; INFO : ... END;
DATA = ARRAY [1..N] OF ITEM;
STATUS = (SEARCHING,FOUND,ENDOFDATA);
WIRD DER TYP VON 'KEY' GEAENDERT, MUSS DER GLEICHE TYP
BEI 'GESUCHT' GENOMMEN WERDEN.
*)
VAR L,R : INTEGER;
BEGIN
L := 1; R := N;
STAT := SEARCHING;
(* BINAERE SUCHE *)
WHILE STAT = SEARCHING DO
BEGIN
POS : (L + R) DIV 2;
IF GESUCHT < D[POS].KEY THEN R := POS - 1 ELSE L := POS + 1;
IF GESUCHT = D[POS].KEY THEN
STAT := FOUND
ELSE
IF L > R THEN STAT := ENDOFDATA;
END;
END;
|
Bild 19. Pascal-Prozedur für binäre Suche. Der Geschwindigkeitsvorteil wird durch die sogenannte „Schlüsseltransformation" erreicht
80000 REM * * * * * * * * * * BINAERE SUCHE * * * * * * * * * *
80001 REM * SUCHE NACH DEM ELEMENT G IM FELD K.
80002 REM * FALLS E=1 DANN IST DAS GESUCHTE ELEMENT
80003 REM * K(P), FALLS E=0 IST G NICHT IM FELD.
80010 L=1
80020 R=N
80030 E=0
80035 REM BEGINN DER SUCHE
80040 P=INT( (L+R)/2 )
80050 IF G<K(P) THEN 80080
80060 L = P + 1
80070 GOTO 80090
80080 R = P - 1
80090 IF G <>K(P) THEN 80110
80100 E=1
80110 IF (E=0) AND (L<=R) THEN 80040
80120 RETURN
80130 REM * * * * * * * * * * * * * * * *
|
Bild 20. Binäre Suche als Basic-Unterprogramm, wieder mit E als Erfolgskriterium
Generieren einer Hash-Tabelle
Das Verfahren der Streuspeicherung (hashing) oder Schlüsseltransformation entstand aus dem Wunsch, ein Element einer Datenmenge mit kleinstmöglichem Aufwand herauszusuchen.
Jedes Element eines Feldes wird bekanntlich durch seinen Feldindex ausgewählt.
Also versucht man eine Abbildung zu finden, die einen Schlüssel auf den Feldindex der zugehörigen Information abbildet.
Anders ausgedrückt: Gesucht ist eine Möglichkeit, den Feldindex aus dem Schlüssel direkt zu berechnen:
Index := F(Schlüssel);
Die Funktion F wird als Hash-Funktion bezeichnet.
Die Schwierigkeit einer derartigen Funktion besteht darin, daß es in der Regel viel mehr mögliche Schlüssel als Feldelemente gibt.
Verwendet man zum Beispiel einen Namen von 20 Zeichen Länge als Schlüssel und rechnet man mit 1000 zu erfassenden Namen, so sind etliche Milliarden Schlüssel auf 1000 Indizes abzubilden.
Weiterhin sollen die Daten auch noch möglichst gleichmäßig auf das Feld verteilt werden, da die Hash-Funktion offensichtlich mehrere Schlüssel auf den gleichen Index abbildet.
Es ergeben sich also die Fragen:
- Wie muß die Hash-Funktion aussehen?
- Wie wird der Fall behandelt, daß die Hash-Funktion zwei vorhandene Schlüssel auf denselben Index abbildet?
Eine Voraussetzung für eine „gute" Hash-Funktion ist, wie gesagt, eine möglichst gleichmäßige Verteilung der Schlüssel auf den Indexbereich und eine möglichst einfache, effiziente Berechenbarkeit:
H(KEY) := KEY MOD N;
wobei N wieder die Feldlänge ist. In der Literatur wird empfohlen, für N eine Primärzahl zu wählen.
Wird für den Schlüssel keine Integer-Größe verwendet, ist noch eine Ordnungsfunktion auf den Schlüssel anzuwenden, die den Schlüssel auf eine Integer-Größe abbildet, d.h. auf eine Ganzzahl-Variable.
H(KEY) := ORD(KEY) MOD N;
Für die Lösung der zweiten Frage ergeben sich mehrere Möglichkeiten:
- Alle Überläufe, das heißt alle Schlüssel, für die der Listenplatz T[H(KEY)] schon belegt ist, werden in einem Feld außerhalb der Tabelle gespeichert.
- Die Überläufe jeder Zeile der Liste T erhalten ein eigenes Überlauffeld.
- Die Überläufe werden in freie Feldelemente von T gespeichert.
Im Programm wurde die letzte Möglichkeit gewählt.
Ist eine Zelle von T besetzt, wird linear weitergesucht, bis eine freie Zelle gefunden wurde oder bis die Liste voll ist.
Dabei wird T als zirkulär betrachtet, das bedeutet, daß auf die letzte Zelle wieder die erste folgt.
Die Liste ist dann voll, wenn bei der Suche das ganze Feld einmal erfolglos durchsucht wurde.
Das Hash-Verfahren ist aus diesem Grund um so effizienter, je mehr freie Zellen zur Verfügung stehen.
Darum sollte die Länge der Tabelle etwa 20% größer gewählt werden, als voraussichtlich für die Daten notwendig ist.
Vor dem Beginn der Listenbearbeitung muß die Liste initialisiert, also mit einem bestimmten Wert vorbesetzt werden, um so die Leerplätze erkennen zu können.
Im folgenden Beispielprogramm soll eine wirklichkeitsbezogene Anwendung gezeigt werden.
Ein Informationssystem wird programmiert
Es soll hier ein Informationssystem für Zeitschriftenaufsätze vorgestellt werden.
Zu jedem Zeitschriftenaufsatz werden ein oder mehrere Stichpunkte zum Inhalt zusammen mit der Heft- und Seitennummer eingegeben.
Dann kann erstens nach bestimmten Stichpunkten gefragt werden, worauf man alle Eintragungen zu dem Stichpunkt erhält oder zweitens eine Liste aller Stichpunkte mit ihren Einträgen ausgegeben werden.
Für das Programm werden benötigt:
- Eingabeprozedur (Aufbau der Liste)
- Abfrageprozedur (Suchen in der Liste)
- Prozeduren zum Abspeichern der Liste auf einer Floppy-Disk-Datei und Wiedereinlesen dieser Datei für spätere Abfragen und Ergänzungen.
Die Datenstruktur des Literatur-Verzeichnisses
Die Datenstruktur für die Tabelle und die Datenspeicherung ist komplizierter als die bisher behandelten Strukturen.
Hier enthält die Hash-Tabelle keine Information, sondern nur einen Verweis auf die Stelle eines Datenfeldes, wo sich die Information befindet.
In Pascal böte sich hier die Verwendung von Zeigern (Pointers) an;
da dieser Datentyp aber in Basic nicht verfügbar ist, wird auch im Pascal-Programm mit Feldern gearbeitet.
Der Grund für die Einführung von Verweisen und einem getrennten Datenfeld liegt darin, daß zu einem Schlüsselwort ja beliebig viele Literaturstellen angegeben werden können.
Es werden alle Literaturstellen (Heft/Seite) in einem linearen Feld gespeichert.
In der Hash-Tabelle werden die Schlüsselworte gespeichert und zu jedem Schlüsselwort eine Zahl, die den Index des Datenfeldes bezeichnet, wo der erste Literaturverweis steht.
Wenn ein neuer Verweis hinzukommt, wird er im Datenfeld angefügt und bei der vorhergehenden Literaturstelle ein Verweis auf diese Stelle eingetragen.
Besser als lange Erklärungen zeigt Ihnen das Bild 21.
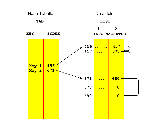
|
|
Bild 21. Die Hash-Tabelle dient als Querverweis-Datenfeld. Sie enthält die Schlüsselworte und die dazu gehörenden Codezahlen
|
Sie sehen schon, das Eintragen wird eine recht aufwendige Sache.
Da aber das Eintragen nur einmal geschieht, die Abfrage aber der Regelfall ist, muß Wert darauf gelegt werden, daß vor allem diese schnell arbeitet.
In Pascal stellt sich die Datenstruktur dann so dar wie in Tabelle 8.
| Tabelle 8: Datentypen-Definition für das Suchprogramm |
|
CONST
N = 499; (* LÄNGE DER HASH-TABELLE *)
LENGTH = 1000; (* LÄNGE DER DATENLISTE *)
TYPE
KEYWORD = PACKED ARRAY [1..30] OF CHAR;
LITERATURVERWEIS = RECORD
HEFT : 0..52;
SEITE: 0..10000;
NEXT : 0..LENGTH
END;
TABLE = ARRAY [0..N] OF RECORD
KEY : KEYWORD;
INFO: 0.. LENGTH
END;
Vereinfacht für Basic:
VAR LIST : ARRAY [1..LENGTH, 1..3] OF INTEGER;
TAB : ARRAY [0..N] OF RECORD
KEY : KEYWORD;
START: 0..LENGTH
END;
|
|
Mit Rücksicht auf die spätere Basic-Version und weil die Seiten- und Heftnummer sowie der Verweis auf den Nachfolger alle Unterbereichstypen von INTEGER sind, wird der Typ LISTE vereinfacht.
Beim Typ LISTE enthält die erste Spalte die Heftnummer, die zweite Spalte die Seitennummer und die dritte Spalte den Verweis auf den Nachfolger.
Falls es keinen Nachfolger gibt, ist der Wert in dieser Spalte leer.
Das Programm und seine Kommandos
Jetzt ist die Planung der Datenstruktur abgeschlossen, und es kann der Grobablauf des Programms festgelegt werden.
Das Programm erwartet vom Bediener die Eingabe eines Kommandobuchstabens, ähnlich wie zum Beispiel ein Editor, und verzweigt dann in das entsprechende Unterprogramm.
Um beim Einfügen von neuen Literaturstellen schnell einen freien Platz zu finden, wird noch eine Variable DATAPOINTER eingeführt, die immer auf das nächste freie Element von LISTE zeigt.
Die Kommandos lauten:
| N | Erzeugen einer leeren Liste (NEW) |
| E | Eintragen neuer Literaturstellen (ENTER) |
| Q | Abfrage nach Einträgen zu einem Keyword (QUESTION) |
| P | Ausdruck aller Keywords mit Literaturstellen (PRINT) |
| S | Beenden des Programms (STOP) |
Beim Programmstart werden Liste und Tabelle von einer Floppy-Disk-Datei eingelesen, beim STOP-Kommando werden sie zurückgeschrieben.
Ist das erste Kommando N, unterbleibt das Einlesen.
Mit Rücksicht auf einige Pascal-Versionen und auf Basic wird für die Listen- und Datendatei eine Datei vom Typ FILE OF CHAR verwendet.
So läßt sich für jede Zeitschrift und jeden Jahrgang eine Datei anlegen und eine Mini-Datenbank erzeugen.
Der Anweisungsteil des Programms läßt sich jetzt schon konstruieren (Tabelle 9).
| Tabelle 9: Anweisungsteil des Literaturverzeichnis-Programms in Pascal |
|
BEGIN
DATAPOINTER := 1;
GENERATENEWLIST;
READ (KOMMANDO);
IF KOMMANDO <> 'N' THEN GETDATA(DATA);
(* JETZT KOMMT EINE PROGRAMMSCHLEIFE, DIE ERST DURCH DAS STOP-
KOMMANDO VERLASSEN WIRD *)
WHILE KOMMANDO <> 'S' DO
BEGIN IF KOMMANDO IN ['E','Q','P','N'] THEN
CASE KOMMANDO OF
'E' : ENTER;
'Q' : QUESTION;
'P' : LISTTABLE;
'N' : GENERATENEWLIST;
END (* CASE *)
ELSE
WRITELN ('ILLEGAL COMMAND, REENTER');
READ (KOMMANDO)
END (* WHILE *);
PUTDATA(DATA);
WRITELN('GOOD BYE')
END.
|
|
Für das Programm werden also sechs Prozeduren verwendet:
GETDATA: Lesen der Liste und der Daten von Datei;
PUTDATA: Zurückschreiben der Liste und der Daten auf Datei;
ENTER: Eingabe neuer Literaturstellen;
QUESTION: Abfrage nach einem Schlüsselwort;
LISTTABLE: Ausdrucken der gesamten Daten;
GENERATENEWLIST: Erstellen einer neuen Liste, Löschen einer alten Liste.
Die einfachste Prozedur ist GENERATENEWLIST:
Sie besetzt alle Schlüssel mit Leerzeichen vor, die Verweise werden mit 1 sowie die Längenangaben und das Datenfeld mit 0 besetzt (Tabelle 10).
| Tabelle 10: Erstellen einer „Leerliste" |
|
PROCEDURE GENERATENEWLIST;
VAR I : 1..LENGTH;
J : 0..N;
BEGIN
FOR I := 1 TO LENGTH DO
FOR J := 1 TO 3 DO LIST [I,J] := 0; (* NÖTIG FÜR PUTDATA *)
FOR J := 0 TO N DO
BEGIN
TAB[J].KEY := '30 Leerzeichen';
TAB[J].START := 1;
END;
END;
|
|
Für das Sichern von Liste und Hashtabelle auf Datei wird für beide Programmversionen das gleiche Format gewählt (Tabelle 11).
| Tabelle 11: Die Pascal-Prozeduren PUTDATA und GETDATA |
|
PROCEDURE PUTDATA (VAR F : TEXT);
VAR I : 1..LENGTH;
J : 0..N;
BEGIN REWRITE (F);
FOR J := 0 TO N DO
WRITELN (F,TAB[J].KEY,' ', TAB[J].START:5);
FOR I := 1 TO DATAPOINTER-1 DO
BEGIN
WRITE (F,LIST[I,1]:6, ' ',LIST[I,3]:6, ' ');
WRITELN(F);
END;
END;
PROCEDURE GETDATA (VAR F : TEXT);
VAR I : 1..LENGTH;
J : 0..N;
K : 1..30;
BEGIN RESET (F);
FOR J := 0 TO N DO
BEGIN (* LESEN TABLE *)
FOR K := 1 TO 30 DO READ (F,TAB[J].KEY[K]);
(* KEY MUSS LEIDER ZEICHENWEISE GELESEN WERDEN *)
READ(F,TAB[J].START); READLN(F);
END;
I := 1;
WHILE NOT EOF[F) DO
BEGIN (* LESEN DER LISTE *)
FOR K := 1 TO 3 DO READ(F,LIST[I,K]);
IF I MOD 5 = 0 THEN READLN(F);
I := I + 1
END;
DATAPOINTER := I;
END;
|
|
Als Nächstes sind nun die Prozeduren zum Einfügen von Literaturverweisen und zum Abfragen oder Auflisten der Daten zu entwickeln.
Um nicht immer einen Schlüssel von vollen 20 Zeichen Länge eingeben zu müssen, wird das Eingabeformat festgelegt als:
Schlüssel, Heft, Seite.
Das ist Format, wie es in Basic standardmäßig verfügbar ist.
In Pascal muß das extra programmiert werden.
Das ist aber eine Absicht des Erfinders von Pascal gewesen.
Der Programmierer soll sehen, was der Rechner tun muß, denn in Basie wird einem nur die Programmierarbeit vom Basic-Interpreter abgenommen, die Arbeit des Rechners ist dieselbe.
Die Eingabe eines Dollarzeichens beendet das Einlesen.
Die Schlüssel werden auf 30 Zeichen Länge gebracht, entweder durch Abschneiden oder durch Auffüllen mit Leerzeichen.
Für die Eingabe einer Zeile wird eine eigene, benutzerfreundliche Prozedur verwendet.
Zunächst wird das Schlüsselwort bis zum Auftreten eines Kommas gelesen; hat es mehr als 30 Zeichen, wird es abgeschnitten;
hat es weniger als 30 Zeichen Länge, wird es mit Leerzeichen aufgefüllt.
Dann werden die Heft- und die Seitennummer gelesen (Tabelle 12).
| Tabelle 12: Prozedur zur Schlüsselwort-Eingabe |
|
PROGEDURE GETLINE (VAR K : KEYWORD; VAR H,S : INTEGER);
VAR I : 0..30;
CH : CHAR; (* ZEICHENPUFFER *)
BEGIN
K := BLANK30;
H := 0; S := 0;
READ(K([1])
IF K[1]<>'$' THEN
BEGIN
I := 1; READ(CH);
WHILE (CH<>',') AND NOT EOLN DO
BEGIN
IF I <30 THEN BEGIN I := I+1; K[I] := CH END;
READ(CH)
END; (* KEYWORD UND KOMMA GELESEN *)
IF NOT EOLN THEN READ(H);
IF NOT EOLN THEN READ(CH); (* KOMMA *)
IF NOT EOLN THEN READ(S);
END;
END;
|
|
Eingescanned von
Werner Cirsovius
September 2002
© Franzis' Verlag

