Suchen und Sortieren in Pascal und Basic
|
1. Teil
In der folgenden Serie sollen die wichtigsten Verfahren zum Sortieren von Daten und zum Suchen nach einem bestimmten Element einer Datenmenge vorgestellt werden.
Die Anwendungsbereiche dafür lassen in ihrer Vielzahl nichts zu wünschen übrig.
Gleichzeitig sind es aber auch die Sortier- und Suchalgorithmen, die die meiste Rechenzeit vieler Programme verschlingen, und so ist gerade hier die Notwendigkeit am größten, einen effizienten Algorithmus zu finden.
Alle hier vorgestellten Algorithmen sind getestete Unterprogramme;
abgefaßt in den beiden Programmiersprachen Pascal und Basic.
Die Verbreitung dieser Sprachen im Mini- und Mikrocomputerbereich läßt fast immer eine direkte Verwendung der Unterprogramme zu.
In allen Programmen wurde auf Klarheit und Übersichtlichkeit geachtet, so daß eine Adaption an einen bestimmten „Dialekt" oder die Übertragung in eine andere Programmiersprache keine Schwierigkeiten bereiten dürfte.
|
Die wichtigsten Anweisungsstrukturen von Pascal und Basic
Die Erläuterung der Algorithmen erfolgt an den Pascal-Unterprogrammen, da bei dieser Sprache die Daten- und Anweisungsstrukturen wesentlich übersichtlicher sind.
Für diejenigen unter Ihnen, denen Pascal nicht so geläufig ist, sind die wichtigsten Anweisungsstrukturen der beiden Sprachen in Tabelle 1 einander gegenübergestellt.
| Tabelle 1: Anweisungsstrukturen |
|
|
Pascal
|
Basic
|
|
IF <Bedingung> THEN
<Anweisung 1>
ELSE
<Anweisung 2>;
|
100 IF <Bedingung> THEN 300
200 <Anweisung 2>
250 GOTO 400
300 <Anweisung 1>
400 REM Hier geht es weiter
|
|
WHILE <Bedingung> DO
<Anweisung>;
|
100 IF NOT <Bedingung> THEN 400
200 <Anweisung>
300 GOTO 100
400 REM Hier geht es weiter
|
|
REPEAT
<Anweisung(en)>
UNTIL <Bedingung>;
|
100 <Anweisung(en)>
200 IF NOT <Bedingung> THEN 100
|
|
FOR <Variable>:=<Wert> TO
<Endwert> DO <Anweisung>;
|
100 FOR <Variable>=<Wert> TO <Endwert>
200 <Anweisung>
300 NEXT <Variable>
|
|
|
<Wert> und <Endwert> können Ausdrücke sein
|
Sollen in Pascal hinter den Schlüsselworten THEN, ELSE oder DO mehrere Anweisungen stehen, so sind diese mit den Schlüsselworten BEGIN und END zu „klammern".
Sie sehen das in den Programmen.
Die Schlüsselworte zur Datendefinition und -Strukturierung (CONST, TYPE und VAR) brauchen Sie als Basic-Programmierer nicht;
die Erklärungen zu den Programmen verwenden sie zwar, sind aber auch für „Nur-Basic-Programmierer" gut zu verstehen.
Alle Pascal-Unterprogramme werden mit dem Schlüsselwort PROCEDURE eingeleitet und die „von außen" kommenden Variablen als Parameter mitgegeben.
So ist zum Beispiel bei der
PROCEDURE SORT (VAR D:DATA);
zum Sortieren der Kundendaten der Aufruf
SORT(KUNDEN);
irgendwo im Hauptprogramm möglich.
Haben die Lieferanten den gleichen Aufbau (die gleiche Struktur) wie die Kunden, können auch diese mit
SORT(LIEFERANTEN);
sortiert werden.
Dieser Prozedurmechanismus hat einen weiteren Vorteil:
Alle innerhalb der Prozedur definierten Variablen haben nur innerhalb der Prozedur Gültigkeit und sind nur dort vorhanden.
Gleichnamige Variablen des Hauptprogramms werden nicht beeinflußt.
In Basic ist ein derartiger Mechanismus nicht verfügbar (leider!).
Datenstrukturen und ihre Realisierung in den beiden Sprachen
Grundsätzlich wird die zu sortierende Information unterteilt in das Such- oder Sortierkriterium (Schlüssel, Key) und die eigentliche Information.
Zum Beispiel ist bei einem Datensatz der Kundendatei der Schlüssel die Kundennummer.
Die Information besteht aus Namen, Adresse, Bankverbindung, offenen Rechnungen usw.
Es ist aber in manchen Fällen möglich, daß der Schlüssel gleichzeitig die einzige Information darstellt (z.B. Namenslisten).
In den Programmen wird als Schlüssel eine Integerzahl (Ganzzahl) verwendet;
sie läßt sich natürlich durch jede andere Datenstruktur ersetzen, die direkte Vergleiche zuläßt.
Als Information wird in den Programmen eine Zeichenkette (String) verwendet.
In Pascal sieht das dann so aus wie in Tabelle 2.
| Tabelle 2: Datentyp-Definition in Pascal |
|
TYPE ITEM = RECORD
KEY : INTEGER;
INFO : PACKED ARRAY [1..10] OF CHAR
END;
|
|
Bei der Variablen des Types ITEM werden durch die Wertzuweisung V1 := V2 alle Teile des Records (also KEY und INFO) von V1 nach V2 gebracht.
Die einzelnen Komponenten von V1 lassen sich durch den Selektionsmechanismus V1.KEY bzw. V1.INFO ansprechen.
In Basic gibt es keine derartige Datenstrukturierungsmöglichkeit.
Es werden hier als Behelf zwei getrennte Variablen verwendet:
K für den Schlüssel (Key)
I$ für die Information (Info)
Ist der Schlüssel gleichzeitig die einzige Information, vereinfacht sich die Struktur natürlich erheblich.
Die einzelnen Datensätze werden in linearen Feldern (Arrays) gespeichert.
So ergeben sich die Programme in Tabelle 3.
| Tabelle 3: Datentypen-Definition im Programm |
|
|
Pascal
|
Basic
|
|
CONST N = 1000; (* Feldlänge *)
TYPE STRING = PACKED ARRAY [1...10] OF CHAR;
TYPE ITEM = RECORD
KEY : INTEGER;
INFO : STRING
END;
DATA : ARRAY [1..N] OF ITEM;
VAR D : DATA;
|
10 N = 1000
20 REM N ist als konstant
30 REM zu betrachten
40 DIM K(1000), I$(1000)
|
|
Programmerstellung, Effizienzvergleich
Es wurde versucht, die Programme so übersichtlich wie möglich und möglichst universell verwendbar zu machen.
So wurde in Basic auf die Besonderheiten bestimmter Dialekte verzichtet.
In den Pascal-Listings wurden die Schlüsselworte (BEGIN, END usw.) aus Gründen der Übersichtlichkeit fett gedruckt.
Ebenso sind in den Programmtext erläuternde Kommentare (*...*) eingefügt.
Der Aufruf der Pascal-Prozeduren erfolgt wie üblich durch den Namen, der Aufruf der Basic-Unterprogramme geschieht einheitlich mit GOSUB.
Für jedes Pascal-Unterprogramm wurde die Effizienz in Form einer Zeitmessung geprüft:
Die Rechenzeit wurde einmal für die Bearbeitung von 100 und einmal für die Bearbeitung von 1000 Feldelementen durchgeführt.
Dabei wurde jeder Datensatz einmal sortiert, einmal umgekehrt sortiert und einmal rein zufällig angeordnet von dem Programm bearbeitet.
Da die Basic-Programme aus den Pascal-Algorithmen entwickelt wurden, lassen sich die Ergebnisse des Effizienzvergleichs der einzelnen Sortierverfahren im Groben auch auf die Basic-Programme übertragen.
Sortieren
Jetzt kann's losgehen - wir haben Datentypen definiert und somit die Grundlage geschaffen, mit diesen Daten irgend etwas anzufangen.
Wenden wir uns zunächst dem Sortieren von Feldern zu.
Später werden wir einen Effizienzvergleich der besprochenen Verfahren anstellen.
Lineares Einfügen
Dieses einfachste aller Sortierverfahren nimmt beginnend bei I=2 das I-te Datenelement und fügt es an der entsprechenden Stelle im Datenfeld ein.
Danach wird I um 1 erhöht und solange fortgefahren, bis alle Datenelemente bearbeitet sind.
Sind nur wenige Daten zu sortieren, hat auch dies einfache Verfahren durchaus seine Berechtigung.
Der Algorithmus lautet also:
FOR I := 2 TO N DO
(* füge den Wert von D[I] an entsprechender
Stelle in D[1]...D[I] ein *)
Das Einfügen geschieht, indem für J von I-1 ausgehend das Element D[I] mit dem Element D[J] verglichen wird und dann entweder D[I] eingefügt oder D[J] nach rechts verschoben wird.
Also muß das Element D[I] vorher auf einer Hilfsvariablen gespeichert werden.
Bild 1 zeigt die Pascal-Prozedur und Bild 2 das Basic-Unterprogramm.
PROCEDURE LINSORT (VAR D : DATA);
(* SORTIEREN DES FELDES D NACH DEN SCHLUESSELN D[..].KEY
IN AUFSTEIGENDER FOLGE.
GLOBALE KONSTANTE : N FELDLAENGE
GLOBALE TYPEN: ITEM = RECORD KEY : ...; INFO : ... END;
DATA = ARRAY [1..N] OF ITEM;
*)
VAR I,J :0..N;
H : ITEM;
ENDE : BOOLEAN;
BEGIN
FOR I := 2 TO N DO
BEGIN
ENDE := FALSE;
H := D[I];
J := I - 1;
WHILE NOT ENDE AND (J>0) DO
IF H.KEY < D[J].KEY THEN (* WEITERSUCHEN *)
BEGIN D[J+1] := D[J]; J := J - 1 END
ELSE ENDE := TRUE;
D[J+1] := H;
END
END (* LINSORT *);
|
Bild 1. Pascal-Programm für lineares Sortieren eines Datenfeldes
10000 REM * * * * * * * * * * LINSORT * * * * * * * * * *
10001 REM * SORTIEREN DES FELDES I$ NACH DEN SCHLUESSELN
10002 REM * IN DEM FELD K.
10003 REM * DIE ELEMENTE K(J) UND I$(J) BILDEN EIN PAAR
10004 REM * SCHLUESSEL - INFORMATION.
10005 REM * DIE UNTERE FELDGRENZE IST 1, DIE OBERE FELD-
10006 REM * GRENZE STEHT IN DER VARIABLEN N.
10010 FOR I = 2 TO N
10020 H$ =I$(I)
10030 H = K(I)
10040 J=I-1
10050 IF H>=K(J) THEN 10100
10060 K(J+1)=K(J)
10070 I$(J+1)=I$(J)
10080 J = J - 1
10090 IF J<>0 THEN 10050
10100 K(J+1) = H
10110 I$(J+1) = H$
10120 NEXT I
10130 RETURN
10140 REM * * * * * * * * * * * * * *
|
Bild 2. Basic-Unterprogramm für lineares Sortieren von Feldvariablen
Binäres Einfügen
Der vorhergehende Algorithmus läßt sich verbessern, indem die bereits vorhandene Ordnung der Elemente D[1] bis D[I] ausgenützt wird, um die Einfügungsstelle zu finden.
Beim binären Einfügen wird in der Mitte der Elemente D[1] bis D[I] geprüft, ob H in der unteren oder in der oberen Hälfte eingefügt werden muß.
Die entsprechende Teilfolge wird wieder halbiert, bis durch die Teilung die Einfügungsstelle gefunden worden ist.
Leider ergibt sich nur eine Reduzierung in der Zahl der Vergleiche, denn der Rest des Programms, also auch die Zahl der Verschiebungen, ist der gleiche wie bei der linearen Sortierung.
Bild 3 enthält das Pascal-Listing, Bild 4 das Basic-Listing.
PROCEDURE BINARYSORT (VAR D : DATA);
(* SORTIEREN DES FELDES D NACH DEN SCHLUESSELN D[..].KEY
IN AUFSTEIGENDER FOLGE.
GLOBALE KONSTANTE : N FELDLAENGE
GLOBALE TYPEN: ITEM = RECORD KEY : ...; INFO : ... END;
DATA = ARRAY [1..N] OF ITEM;
*)
VAR I,J,L,R,M : 0..N;
H : ITEM;
BEGIN
FOR I := 2 TO N DO
BEGIN
J := I - 1;
L := 1; R:=J;
H := D[I];
WHILE L <= R DO (* BINAERE SUCHE *)
BEGIN
M := (L + R) DIV 2;
IF H.KEY < D[M].KEY THEN R := M - 1 ELSE L := M + 1;
END;
WHILE J >= L DO (* VERSCHIEBEN *)
BEGIN D[J+1] := D[J]; J :=J - 1 END;
D[L] := H;
END;
END (* BINARYSORT *);
|
Bild 3. Sortieren durch binäres Einfügen in Pascal
20000 REM * * * * * * * * * * BINARY SORT * * * * * * * * * *
20001 REM * SORTIEREN DES FELDES I$ NACH DEN SCHLUESSELN
20002 REM * IN DEM FELD K.
20003 REM * DIE ELEMENTE K(J) UND I$(J) BILDEN EIN PAAR
20004 REM * SCHLUESSEL - INFORMATION.
20005 REM * DIE UNTERE FELDGRENZE IST 1, DIE OBERE FELD-
20006 REM * GRENZE STEHT IN DER VARIABLEN N.
20010 FOR I = 2 TO N
20020 L=1
20030 R= I - 1
20040 H$ = I$(I)
20050 H = K(I)
20060 REM * * * BINAERE SUCHE * * *
20070 IF L>R THEN 20140
20080 M= INT( (L+R)/2 )
20090 IF H<K(M) THEN 20120
20100 L=M+1
20110 GOTO 20070
20120 R = M-1
20130 GOTO 20070
20140 FOR J = I-1 TO L STEP -1
20150 I$(J+1) = I$(J)
20160 K(J+1) = K(J)
20170 NEXT J
20180 I$(L) = H$
20190 K(L) = H
20200 NEXT I
20210 RETURN
20220 REM * * * * * * * * * * * * * * * *
|
Bild 4. Basic-Programm zum Sortieren durch binäres Einfügen
Bubblesort und Shakersort
Bei diesen beiden Verfahren wird wie bei den vorhergehenden das Feld mehrfach durchlaufen.
Anstelle des Einfügens des entsprechenden Feldelements an der richtigen Stelle wird hier das jeweils kleinste Element durch Austausch mit dem Nachbarn an die passende Stelle gebracht.
Wenn man das Feld vertikal aufschreibt, „perlt" das Feldelement nach oben an seinen Platz, und das hat diesem Verfahren den Namen eingetragen.
In der Pascal-Version wird der Austausch durch die Prozedur SWAP erledigt, in der Basic-Version sind die Operationen in das Programm eingefügt (Bild 5 und Bild 6).
PROCEDURE BUBBLESORT(VAR D : DATA);
(* SORTIEREN DES FELDES D NACH DEN SCHLUESSELN D[..].KEY
IN AUFSTEIGENDER FOLGE.
GLOBALE KONSTANTE : N FELDLAENGE
GLOBALE TYPEN: ITEM = RECORD KEY : ... INFO : .... END;
DATA = ARRAY [1..N] OF ITEM;
*)
VAR J,I : 0..N;
PROCEDURE SWAP(VAR X,Y : ITEM);
VAR Z : ITEM;
BEGIN Z := X; X := Y; Y := Z END;
BEGIN
FOR I := 2 TO N DO
FOR J := N DOWNTO I DO
IF D[J-1].KEY > D[J].KEY THEN SWAP(D[J],D[J-1]);
END (* BUBBLESORT *);
|
Bild 5. Pascal-Prozedur für „Bubblesort" (Blasen-Sortieren)
30000 REM * * * * * * * * * * BUBBLESORT * * * * * * * * * *
30001 REM * SORTIEREN DES FELDES I$ NACH DEN SCHLUESSELN
30002 REM * IN DEM FELD K.
30003 REM * DIE ELEMENTE K(J) UND I$(J) BILDEN EIN PAAR
30004 REM * SCHLUESSEL - INFORMATION.
30005 REM * DIE UNTERE FELDGRENZE IST 1, DIE OBERE FELD-
30006 REM * GRENZE STEHT IN DER VARIABLEN N.
30010 FOR I = 2 TO N
30020 FOR J = N TO I STEP -1
30030 IF K(J-1)>K(J) THEN 30050
30040 GOTO 30110
30050 H$ = I$(J)
30060 H = K(J)
30070 I$(J) =I$(J-1)
30080 K(J) = K(J-1)
30090 I$(J-1) = H$
30100 K(J-1) = H
30110 NEXT J
30120 NEXT I
30130 RETURN
30140 REM * * * * * * * * * * * * * * * *
|
Bild 6. Bubblesort auf einem Basic-Computer
Wenn Sie den Algorithmus auf die Möglichkeit der Verbesserung hin untersuchen, fällt Ihnen sicher gleich die feste Schleifenstruktur auf, die keine Rücksicht auf schon sortierte Sequenzen nimmt.
Die erste Verbesserung ist dadurch möglich, wenn das Programm abbricht, wenn das Feld sortiert ist.
Das ist der Fall, wenn in einem Durchlauf für I kein Austausch erfolgte.
Weiterhin ist Bubblesort höchst asymmetrisch, wenn Sie zum Beispiel die beiden folgenden Felder betrachten, können Sie feststellen, daß D1 schon nach einem Durchlauf, D2 dagegen erst nach sieben Durchläufen sortiert ist.
D1: 10 25 36 54 87 2
D2: 87 2 10 25 36 54
Die Asymmetrie läßt sich beseitigen, indem in aufeinanderfolgenden Durchläufen jeweils in entgegengesetzter Richtung gearbeitet wird.
Dieses „Auf" und „Ab" hat dem Verfahren auch zu dem Namen Shakersort verholfen.
Eine letzte Verbesserung ergibt sich, wenn man den Index festhält, bis zu dem das Feld schon sortiert ist.
Das Ergebnis der Verbesserung von Bubblesort finden Sie in Bild 7 und Bild 8.
PROCEDURE SHAKERSORT (VAR D : DATA);
(* SORTIEREN DES FELDES D NACH DEN SCHLUESSELN D[..].KEY
IN AUFSTEIGENDER FOLGE.
GLOBALE KONSTANTE : N FELDLAENGE
GLOBALE TYPEN: ITEM = RECORD KEY : ...; INFO : ... END;
DATA = ARRAY [1..N] OF ITEM;
*)
VAR I,J,R,L : 0..N;
PROCEDURE SWAP(VAR X,Y : ITEM);
VAR Z : ITEM;
BEGIN Z := X; X := Y; Y := Z END;
BEGIN
L := 2; R := N; I := N - 1;
REPEAT
FOR J := R DOWNTO L DO (* RAUFSCHUETTELN *)
BEGIN
IF D[J-1].KEY > D[J].KEY THEN
BEGIN SWAP(D[J],D[J-1]); I := J (* INDEX MERKEN *) END;
END;
L := I + 1;
FOR J := L TO R DO (* RUNTERSCHUETTELN *)
BEGIN
IF D[J-1].KEY > D[J].KEY THEN
BEGIN SWAP(D[J],D[J-1]); I :=J (* INDEX MERKEN *) END;
END;
R := I - 1;
UNTIL L > R;
END;
|
Bild 7. Pascal-Prozedur für „Shakersort"
40000 REM * * * * * * * * * * SHAKERSORT * * * * * * * * * *
40001 REM * SORTIEREN DES FELDES I$ NACH DEN SCHLUESSELN
40002 REM * IN DEM FELD K.
40003 REM * DIE ELEMENTE K(J) UND I$(J) BILDEN EIN PAAR
40004 REM * SCHLUESSEL - INFORMATION.
40005 REM * DIE UNTERE FELDGRENZE IST 1, DIE OBERE FELD-
40006 REM * GRENZE STEHT IN DER VARIABLEN N.
40010 L = 2
40020 R = N
40030 I = N - 1
40040 REM BEGINN DER REPEAT- SCHLEIFE, ENDE BEI 40170
40050 FOR J = R TO L STEP -1
40060 IF K(J-1) <= K(J) THEN 40090
40070 GOSUB 40190
40075 REM GO AND SWAP D(J) WITH D(J-1)
40080 I = J
40090 NEXT J
40100 L = I + 1
40110 FOR J = L TO R
40120 IF K(J-1)<=K(J) THEN 40150
40130 GOSUB 40190
40140 I = J
40150 NEXT J
40160 R = I - 1
40170 IF L <= R THEN 40040
40180 RETURN
40190 REM * * SWAP (D(I),D(J-1))
40200 H$ = I$(J)
40210 H = K(J)
40220 I$(J) = I$(J-1)
40230 K(J) = K(J-1)
40240 I$(J-1) = H$
40250 K(J-1) = H
40260 RETURN
40270 REM * * * * * * * * * * * * * * * *
|
Bild 8. Basic-Unterprogramm für das Shaker-Sortierverfahren
Im übrigen sind von Bubblesort und Shakersort keine besonders große Verbesserungen zu erwarten.
Shakersort ist jedoch bei weitgehend sortierten Feldern zu empfehlen.
Mit diesen beiden Verfahren sind die einfachen Sortiermethoden abgeschlossen.
Die beiden folgenden sehr effizienten Sortierverfahren sind in ihrem Algorithmus wesentlich komplizierter und finden hauptsächlich dann Anwendung, wenn es darum geht, sehr große Datenmengen zu sortieren.
Heapsort
Die bisher behandelten Algorithmen suchten immer nur ein Element, das kleinste aus der Restmenge von N-1 Elementen heraus.
Die Sortiermethode läßt sich also nur beschleunigen, indem bei einem Durchlauf mehr Information gesammelt wird.
Eine Sortiermethode, die nach diesem Schema verfährt, ist das Sortieren mit Bäumen.
Dabei wird als Baum die unten gezeigte Anordnung der Elemente einer Datenmenge bezeichnet.
Betrachten Sie dazu die Folge von Schlüsseln:
40 50 10 45 90 15 5 65
Ordnet man diese Elemente in einem Baum derart, daß immer das kleinere Element als Wurzel verwendet wird, benötigt man N-1 Vergleiche (Bild 9).
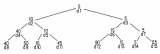
|
|
Bild 9. Beim Heap-Sortierverfahren benötigt man für N Elemente stets N-1 Vergleiche
|
Wenn ein solcher binärer (= zweiästiger) Baum in einem linearen Feld gespeichert werden soll, ergibt sich die Bedingung:
d [i] <= d [2i] und d [i] <= d [2i+1]
(Die Feldkomponenten stehen unter den Schlüsseln.)
Eine derartige Anordnung der Schlüssel heißt HEAP.
Angenommen, der Heap (Bild 10) soll um ein Element (d1 = 40) erweitert werden.
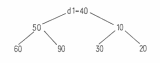
|
|
Bild 10. Erweiterung eines „Heap" um das Element d1 = 40
|
Das neue Element (z.B.: d1 = 40) wird zuerst einmal an die Spitze gesetzt.
Dann läßt man es entlang der kleineren Elemente nach unten wandern, wobei die kleineren Elemente gleichzeitig nach oben steigen (Bild 11).

|
|
Bild 11. Sortierschritte beim Einfügen des neuen Elements 40
|
Das Sortierverfahren von Heapsort (
Tabelle 4) besteht also aus zwei getrennten Tätigkeiten:
- Aufbau des Heap aus den Feldelementen (im Programm: IF L<1);
- Abarbeiten des Heap (im Programm: ELSE).
| Tabelle 4: Pascal-Programm HEAPSORT |
|
PROCEDURE HEAPSORT (VAR D : DATA);
.
.
.
BEGIN
L := (N DIV 2) + 1; (* BINAERER BAUM! *)
R := N;
REPEAT
IF L>1 THEN
(* HEAP AUFBAUEN *)
L:=L-1
ELSE
IF R>1 THEN
(* HEAP ABARBEITEN *)
BEGIN SWAP (D[L], D[R]); R := R-1 END;
(* NAECHSTES HEAPELEMENT DURCH DEN HEAP
WANDERN LASSEN, SIEHE OBEN *)
UNTIL R =1
END;
|
|
Die fertige Prozedur ist in Bild 12, das entsprechende Basic-Programm in Bild 13 aufgelistet.
PROCEDURE HEAPSORT (VAR D : DATA);
(* SORTIEREN DES FELDES D NACH DEN SCHLUESSELN D[..].KEY
IN AUFSTEIGENDER FOLGE.
GLOBALE KONSTANTE : N FELDLAENGE
GLOBALE TYPEN: ITEM = RECORD KEY : ...; INFO : .... END;
DATA = ARRAY [1..N] OF ITEM;
*)
VAR I,J,R,L : INTEGER;
H : ITEM;
CONTINUE : BOOLEAN (* STOPPER FUER DIE WANDERUNG *);
PROCEDURE SWAP(VAR X,Y : ITEM);
VAR Z : ITEM;
BEGIN Z := X; X := Y; Y := Z END;
BEGIN
L := (N DIV 2) + 1; R := N;
REPEAT
IF L > 1 THEN
L := L - 1
ELSE
IF R > 1 THEN
BEGIN SWAP(D[L],D[R]); R := R - 1; END;
(* WANDERN DES NAECHSTEN ELEMENTS DURCH DEN HEAP *)
I := L; J := 2*I;
H := D[I];
CONTINUE := J <= R;
WHILE CONTINUE DO
BEGIN
IF J < R THEN (* DANN DARF D[J] MIT D[J+1] VERGLICHEN WERDEN *)
IF D[J].KEY < D[J+1].KEY THEN J := J + 1;
IF J<=R THEN (* VERGLEICH H<D[J].KEY ZULAESSIG *)
CONTINUE := H.KEY < D[J].KEY ELSE CONTINUE := FALSE;
IF CONTINUE THEN
BEGIN (* EINORDNEN *)
D[I] := D[J];
I := J; J := 2*I ;
END;
END (* WHILE CONTINUE *);
D[I] := H;
UNTIL R = 1;
END (* HEAPSORT *);
|
Bild 12. Die fertige Heapsort-Prozedur in Pascal
50000 REM * * * * * * * * * * HEAPSORT * * * * * * * * *
50001 REM * SORTIEREN DES FELDES I$ NACH DEN SCHLUESSELN
50002 REM * IN DEM FELD K.
50003 REM * DIE ELEMENTE K(J) UND I$(J) BILDEN EIN PAAR
50004 REM * SCHLUESSEL - INFORMATION.
50005 REM * DIE UNTERE FELDGRENZE IST 1, DIE OBERE FELD-
50006 REM * GRENZE STEHT IN DER VARIABLEN N.
50010 L = INT(N/2) + 1
50015 REM IN PASCAL L = N DIV 2+ 1
50020 R = N
50030 IF L>1 THEN 50130
50035 REM BAUM AUFBAUEN
50040 IF R<=1 THEN 50120
50050 H$=I$(L)
50060 H = K(L)
50070 I$(L)=I$(R)
50080 K(L)=K(R)
50090 I$(R)=H$
50100 K(R)=H
50110 R=R - 1
50120 GOTO 50140
50130 L=L-1
50140 REM W A N D E R N
50150 I=L
50160 J=2*I
50170 H=K(I)
50180 H$=I$(I)
50190 IF J>R THEN 50280
50200 IF J>=R THEN 50220
50205 IF K(J)>=K(J+1) THEN 50220
50210 J = J + 1
50220 IF J>R THEN 50280
50225 IF H>=K(J) THEN 50280
50230 I$(I)=I$(J)
50240 K(I)=K(J)
50250 I=J
50260 J=2*I
50270 GOTO 50200
50280 I$(I)=H$
50290 K(I)=H
50300 IF R<> 1 THEN 50030
50310 RETURN
50320 REM * * * * * * * * * * * * * * * *
|
Bild 13. Heapsort läßt sich auch in Basic relativ einfach programmieren
Diese Prozedur hat noch eine schöne Eigenschaft.
Wenn man bei den zwei Zeilen
IF D[J].KEY<D[J+1].KEY THEN J:=J+1;
CONTINUE := H.KEY<D[J].KEY ELSE
CONTINUE := FALSE;
die Kleinerzeichen durch Größerzeichen ersetzt, wandert das größere Element nach oben und das Feld wird dann absteigend, also genau umgekehrt sortiert; im Basic-Programm sind das die Zeilen 50205 und 50225.
Als letztes Sortierverfahren folgt im nächsten Heft Quicksort.
Eingescanned von
Werner Cirsovius
September 2002
© Franzis' Verlag
