|
The following article was printed in April 1985 of the magazine „Computer Language".
|
An article referring to searching by dispersion.
|
|
Sorting by
Dispersion
 Computer journals have recently published a number of articles on sorting algorithms.
The authors have usually favored the comparison method used in the Shell sort and in C.A.R.Hoare's Quicksort.
Some have noted as well ihe existence of the distribution or dispersion method, which also goes under the names of hash coding, address calculation, bulldozer sort, and range sorting.
Computer journals have recently published a number of articles on sorting algorithms.
The authors have usually favored the comparison method used in the Shell sort and in C.A.R.Hoare's Quicksort.
Some have noted as well ihe existence of the distribution or dispersion method, which also goes under the names of hash coding, address calculation, bulldozer sort, and range sorting.
Sorts using the comparison method arrange elements of an array, such as words, in ascending lexicographical order by repeated comparisons of selected elements, two at a time.
The processing exchanges elements that are found to be out of order with respect to each other.
After the program has compared each element with a certain number of other elements in the array and made the appropriate exchanges, it can be determined that the entire array has been sorted.
An alternative approach
The dispersion method makes an initial pass through the array, evaluating each element in some way and putting a vector into internal storage at a location corresponding to the value of the clement.
This vector points to the element.
The algorithm then retrieves all the pointers in their new, sorted order.
That is the procedure, roughly sketched.
We may try to sort a small mailing list according to zip code, for example, by assigning each record to one of a thousand pointers.
The subscript in the pointer array will be the value of the first three digits of the zip code in the corresponding record.
After the pointer array has been cre-
ated, we may run through it, collecting
nonzero pointers and thus gaining access
to the records they point to. They will be
in perfect order by the first three digits of
the zip code.
If two records' zips have the same first three digits, however, we have a problem:
room must be made for two pointers that, according to the rules, should have the same subscript.
One solution is to assign the record to a location one higher or one lower than the corresponding three-digit zip value.
Additional displacements may be made in case there is still a collision.
Provided the number of such collisions is low, the extra time required to move a pointer up or down the array — before depositing it where it will lie until collection time — will be well spent, because a dispersion-based sort can be very fast, as will be seen later on.
But if our mailing list happens to be entirely from the same region, the large number of collisions will cause the sort to take a very long time — longer than the Shell sort or Quicksort.
A possible solution to the collision problem is to create a very large array with plenty of room for colliding pointers.
Instead of shifting hundreds of pointers up or down the pointer array to make room for one new pointer, we might displace a pointer into one of the extra slots, of which there will be plenty.
If we were manually sorting index cards with names on them, we might use such a method.
We could put cards on a table with plenty of space between them to make room for yet-to-be-encountered
cards.
Such a solution entails plenty of table space — or, in a computer, high-memory overhead.
Harold Lorin's Sorting and Sort Systems (p. 152) states that for certain implementations, "the algorithm requires space for the representation of 2(A*N) elements," where N is the size of the array being sorted and A is the number of possible values for a character position.
(If numbers were being sorted, A would be 10; if words composed of letters of our alphabet were being sorted, A would be 26.)
In other words, if we were sorting 50 index cards into groups according to the first letter of the name on each card, we would need table space for 26 times 50, or 1,300 cards, to cover the possibility that all the cards will be in the same group.
Sometimes data that must be sorted has more or less randomly-distributed key values.
For these, the simple "address-calculation" sort described by Douglas Davidson in BYTE (November 1983) will be adequate.
But if we are sorting names, text words, or even zip codes, we will almost certainly find a highly nonrandom distribution.
We will find clumps of Smiths and Jones's that will cause large numbers of collisions and hence turn a fast sort into a slow one.
This article will present a way to solve the problem of quickly sorting unevenly distributed data in a memory space not substantially greater than that required to hold the array being sorted.
In other words, it will describe a way to avoid the time-consuming processing of collisions without using a large extra amount of memory.
Why dispersion can sort faster
First let us examine the comparison approach and see what its limits are.
The graph in
Figure 1 indicates how the Shell sort, a fast, comparison-based algorithm, requires increasing amounts of time per element to sort increasingly large arrays.
Because the X coordinate (Size of array (N)) on the graph is scaled logarithmically, with a base of two, we can easily see that the Shell sort log2N an execution time proportional to log2N process each element; the curve approximates a straight line originating at zero.
As Donald Knuth has shown, sorting algorithms based on comparisons cannot execute faster than this — he total time is at best proportional to N*log2N.
(That is, at least log2N comparisons must be made for each element.)
This is because a comparison yields only one bit of information: either the left element is greater than the right or it is not; either an exchange must be made or no exchange is to be made.
For each doubling of the size of the array to be sorted, an extra pass is required, comparing each element to some other element.
By the time we're sorting about 16,000 elements, about 13 passes through the whole array will be necessary: 213 = 16,384.
The way to flatten the graph and decrease the number of passes necessary is to extract more than one bit of information from each examination of an element.
String data yields eight bits of information just by an examination of the first eight-bit character.
Words composed of letters of our alphabet yield about five bits by such an examination; that is, the first letter can be anything from A to Z if capital and lower-case letters are assigned the same value.
26, the number of letters in our alphabet, is approximately 25.
Increasing in this way the number of bits of information extracted in examining an element means that instead of needing an extra pass each time the array size is doubled, we will require an additional two-way pass only after the size of the array increases 26-fold.
In other words, if we extract information from the first character of a word string, rather than comparing strings, our goal can be a sort-timc-per-element figure proportional to log26N.
For 17,000 elements, log26N is only about 3.
This means that six passes are necessary for such a sort: three to distribute elements and three to collect.
Six passes are fewer than half as many as 13, the number of passes required to sort 16,000 elements with a comparison-based algorithm.
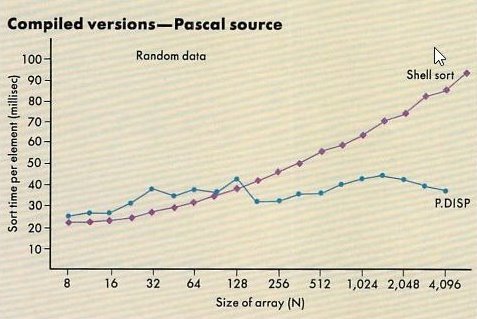
Figure 1.
Test results
Observe Figures 1 and 2.
Here we find that the performance of some dispersion-based algorithms (called P.DISP in
Figure 1 and DISP.1 and DISP.2 in
Figure 2)
have slopes that arc consistent with this general theoretical prediction.
The dispersion algorithm sorts large numbers of random array elements almost twice as fast as the Shell algorithm.
If we extrapolated the performance figures shown, we could predict that tens or hundreds of thousands of random elements can be sorted, using dispersion, in only slightly more time per clement than is necessary 10 sort hundreds of elements.
That is, total sorting time is very close to being proportional to the number of elements sorted.
The dispersion sort illustrated not only performs roughly twice as fast as Shell in the 3,000-to-6,000-element range, it promises to perform better and better in comparison with Shell or any other comparison-based sort as the number of elements to be sorted rises.
It is moreover not adversely affected by preordering of arrays (as is Quicksort), and it is not highly sensitive to unevenly distributed data.
Compare DISP.2 sorting text data in
Figure 2 with the two sorts of random data.
(DISP.1 and DISP.2 are similar dispersion sorts.)
The strings used in the text data were the words from a scene in "Hamlet, Prince of Denmark" whereas the other samples were randomly generated, three-letter strings.
Performance with nonrandom word strings was not qualitatively slower than with random strings in the 50-to-1,600-element range.
This dispersion algorithm is thus a general purpose one, requiring no special inspection of the data before use.
It is
designed in such a way that its worst-case performance will be comparable to the performance of the Shell sort, and its best-case performance will be much, much faster than Shell.
One dispersion algorithm
The Pascal listing, P.DISP, presented in
Listing 1 shows the logic of one of the algorithms whose performance was graphed in
Figure 2.
Exactly the same logic was used in the BASIC program DISP.1, and the logic in DISP.2 was almost identical.
Five modules of P.DISP are relevant to our discussion:
the main routine; the segment-processing routine, ProcSeg; the pointer-dispersing routine, Distribute; the pointer-collecting routine, Collect; and the Shell-sort routine, Shell, which is used as part of the dispersion algorithm.
Two other procedures, Create and Report, come into use only to generate random string data, time the test, and display the results.
To sort our array of random three-letter words, the program first examines each element and puts it into one of 27 "bins" where it can be retrieved.
P.DISP does this by beginning with a segment consisting of the entire array.
ProcSeg processes this segment, first calling Distribute to allocate the elements among 27 linked lists according to the letter of the alphabet with which the word begins.
An extra twenty-seventh bin will accept words not beginning with a letter of the alphabet.
The linked lists are one key to the success of the algorithm.
Instead of creating
27 arrays, each dimensioned to the maximum number of elements to be sorted, N, our algorithm creates one array of 27 elements, called Anchor, and an array of N integer links.
Anchor(1) is a pointer pointing to the first clement beginning with "a"; Anchor(2) points to the first "b" word, etc.
To insert a second "a" word into the linked list, the word's subscript is assigned to Anchor(1).
Anchor(1) acquires a link that points to the previous occupant of Anchor(1).
Further additions to the "a" bin are accomplished by replacing Anchor(1) and by linking the new occupant of Anchor(1) to its old occupant.
The "a" bin, a linked list, has the capacity to contain all the elements in the array to be sorted, if necessary.
Twenty-seven such linked lists are created by Distribute.
A way to understand the linked lists in P.DISP is to picture a row of 27 hooks on the wall.
We hang an "a" word from the "a" hook.
The "a" word has a hook hanging from it as well.
To add a new "a" word, we take the top word off the hook on the wall, replace it with the new word, and hang the old top word from the new word's hook.
More words are added in the same way, at the top.
Why add words at the top and not at the bottom of the chain?
Because to access the bottom of a linked list in computer memory, we must examine each link to learn what the next element will be.
Adding to the top allows us to avoid a possibly long series of examinations each time a new element is added to the list.
This brings us to the next step of the dispersion sort, the collection routine — Collect in the Pascal program illustrated here.
Again, each chain is removed from the wall and the words are taken off the top of the chain in order.
The linked lists here are employed as stacks, not as queues; the last "a" word added is the first retrieved.
In this way the collect module may retrieve each element in one short step.
As the bins are emptied, A through Z, their pointer contents are assigned to an n-element pointer array.
If each bin has only one element in it, or none, our entire array has been sorted in one step.
If not, we must perform further processing, because Distribute and Collect do not sort within bins, only among them.
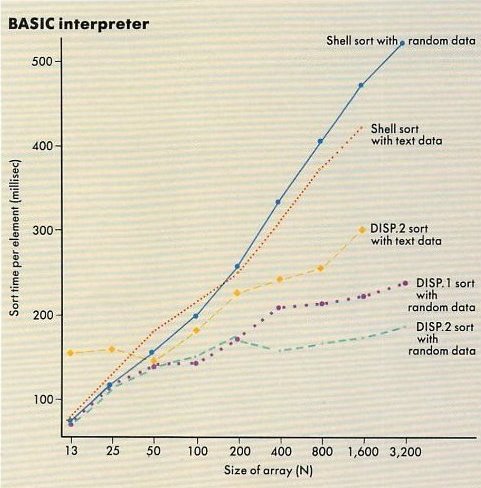
Figure 2.
To sort within a bin, as is required whenever the bin contents number more than one, our algorithm selects one of two paths.
If a bin's size is less than nine, Collect calls Shell, which sorts the contents of the bin by the comparison method.
Nine is an arbitrary choice.
We use Shell here because it sorts small arrays faster than a dispersion sort.
(A Bubble sort in place of the Shell sort might sort the nine or fewer element bins in even less time.)
If the size of the bin is greater than nine, we consider it, after retrieval, as a segment, saving its beginning and end locations in the overall pointer array as LO and HI for that segment.
The depth at which the program is examining the data array — one if the first letter of each element is being evaluated, two if the second, etc. — is saved as DEPTH for the new segment.
Then we continue collecting the contents of bins until the twenty-seventh is emptied.
On completion of Collect, control proceeds to the next segment.
If the first segment was the entire array to be sorted, the second is the first bin that contains more than nine elements.
Just as we have sorted the entire array into 27 bins in processing the first segment, the processing of the second segment sorts one of the resulting bins into 27 bins.
Our program distributes and collects the contents of this second segment, examining the second character of each word.
If the "b" bin was the first to contain more than nine elements on the first pass, then "bat," "baffle," and "bar" will end up in the first bin, the "a" bin, of this second distribulion and collection.
Through use of the method known as tail recursion, the entire array is repeatedly subdivided in this way into bins until it has been fully sorted.
If a bin is collected that results from a distribulion on the third character and still has more than nine pointers in it, then it is Shell sorted rather than saved as a segment to be distributed and collected on the fourth character.
There is no point in trying to distribute and collect on the fourth character because our random tesi data words contain only three characters each.
If all the elements in a segment fall into the same bin, then we Shell sort that bin rather than distribute it again, because we are in a situation where it seems likely that examinations of the next character bin will only yield more bins containing all the elements, as would be the case with a long list of Smiths.
Using a range table
We have examined here only one way to use the dispersion technique in a general purpose sort.
Improvements are not hard to imagine; one example is a range table that allocates words among bins according to an examination of two or three characters at a time.
Calculating the bin number for a distribution on two characters would require 27*27, or 729 bins, and most would probably end up empty, such as all the bins containing words beginning with "x" and another consonant.
A much smaller number of bins would be needed if a good range table were used, because only a small proportion of these 729 combinations of letters actually occur in English-language names and text words.
Rather than yielding four or five bits of information, as an examination of one letter does, an examination of two letters, using a range table to choose a bin number, would yield perhaps eight bits (256 bins).
In that case, we might aim for a much greater speed than is possible with the algorithm presented in P.DISP.
Whereas P.DISP requires six passes to sort 16,000 randomly chosen strings, up to 64K English-language words could be sorted in four passes if the range table yielded eight bits of information per examination.
The dispersion method is known to the computer world but seems to have been rarely applied with microcomputers due to the greater complexity of the algorithms, the higher memory overhead (a factor sometimes overestimated), and the only marginal speed advantage at array sizes below about a thousand.
An additional factor may be that fast algorithms are undoubtedly often kept as business secrets.
As hard disks become more widespread and RAM chips of greater capacity come into use, it seems likely that dispersion-based sorting algorithms will tend to replace algorithms based on comparison.
In spelling-checker programs, for example, a fast sort of words in RAM will mean a very fast check and much-improved response, to the benefit of users.
That is pan of what the present generation of computers and software is all about.

David Keil works in computer interfaced typesetting at Crackergraphics, Needham, Mass.
He has a B.A. in history from the Univ. of Minnesota.
PROGRAM P.DISP (DISPERSION SORT);
(**)
VAR L,E,B,I,X,POINTER,SEGMENT,LAST,T1,T2,T3,LETTER: INTEGER;
TI: REAL;
P,LINK: ARRAY[1..4096] OF INTEGER;
ANCHOR: ARRAY[1..27] OF INTEGER;
HI,LO,DEPTH: ARRAY[1..60] OF INTEGER;
ELEMENT: ARRAY[1..4096] OF STRING[3];
(* CREATETESTDATA *)
PROCEDURE CREATE (X: INTEGER);
BEGIN
MEM[$D021]:= CHR(0);
WRITE(CHR(147),CHR(5),CHR(14));
FOR I := 1 TO 27 DO
ANCHOR[I] := 0;
WRITE('NO. OF ELEMENTS? ');
READ(L);
FOR I := 1 TO L DO
BEGIN
T1:= TRUNC(65+26*ABS(RND(1)));
T2:= TRUNC(65+26*ABS(RND(1)));
T3:= TRUNC(65+26*ABS(RND(1)));
ELEMENT[I]:= CONCAT(CHR(T1),CHR(T2),CHR(T3));
WRITE(ELEMENT[I],' ');
P[I]:= I;
LINK[I] := 0;
END;
MEM[$00A0] := CHR(0); MEM[$00A1] := CHR(0); MEM[$00A2] := CHR(0);
SEGMENT:= 0; LAST:= 1; LO[1]:=1; HI[1]:= L; DEPTH[1]:= 1;
END;
(* DISTRIBUTE ELEMENTS -)
PROCEDURE DISTRIBUTE (B,E: INTEGER);
VAR WORD: STRING;
SEGDEPTH: INTEGER;
LETCHAR: CHAR;
BEGIN
SEGDEPTH := DEPTH[SEGMENT];
FOR I:= B TO E DO
BEGIN
LETCHAR := COPY(ELEMENT[P[I]],SEGDEPTH,1);
LETTER := ORD(LETCHAR)-64;
LINK[P[I]] := ANCHOR[LETTER];
ANCHOR[LETTER] := P[I];
END
END;
(* SHELLSORT *)
PROCEDURE SHELL (B.E: INTEGER);
VAR D,SL,J,T,FIRST,SECOND: INTEGER;
BEGIN
SL:= E-B+1;
D:= TRUNC(EXP(TRUNC(LN(SL)/LN(2))*LN(2)))-1;
WHILE D>=1 DO
BEGIN
I := B;
WHILE I<=E-D DO
BEGIN
J := I;
WHILE J>=B DO
BEGIN
FIRST := P[J]; SECOND := P[J+D];
IF ELEMENT[FIRST] > ELEMENT[SECOND]
THEN BEGIN
T:= P[J]; P[J]:= P[J+D]; P[J+D]:= T; J:= J-D;
END
ELSE J:= 0;
END;
I:= I+1
END;
D:= TRUNC(D/2);
END;
END;
(* COLLECTELEMENTS *)
PROCEDURE COLLECT (BEGSEG: INTEGER);
BEGIN
I := BEGSEG-1;
FOR LETTER := 1 TO 27 DO
BEGIN
B:= I+1;
IF ANCHOR[LETTER] > 0 THEN
BEGIN
I := I+1;
P[I] := ANCHOR[LETTER];
ANCHOR[LETTER] := 0;
WHILE LINK[P[I]]> 0 DO
BEGIN
I := I+1;
P[I] := LINK[P[I-1]];
LIKK[P[I-1]] := 0;
END;
IF I-B > 9
THEN
IF (B = BEGSEG) OR (DEPTH[SEGMENT] > 2)
THEN
SHELL(B,I)
ELSE
BEGIN
LAST:= LAST + 1;
LO[LAST]:= B; HI[LAST]:= I; DEPTH[LAST] := DEPTH[SEGMENT] + 1;
END
ELSE
IF I > B
THEN SHELL(B,I);
END
END
END;
(* PROCESSSEGMENT *)
PROCEDURE PROCSEG (X: INTEGER);
BEGIN
WRITE(SEGMENT,' ');
DISTRIBUTE (LO[SEGMENT],HI[SEGMENT]);
COLLECT (LO[SEGMENT]);
END;
(* PRINTRESULTS *)
PROCEDURE REPORT (L: INTEGER);
BEGIN
T1 := ORD(MEM[$00A0]); T2 := 0RD(MEM[$00A1]); T3 := 0RD(MEM[$00A2]);
T1 := 1092.26*T1+4.26667*T2+T3/60;
WRITELN(CHR(13),L,' ELEMENTS',CHR(13),'TIME: ' ,TRUNC(100*T1+0.5)/100) ;
WRITELN('MILLISEC/ELE: ',TRUNC(1000*T1/L+0.5)) ;
WRITELN('PRESS RETURN'); READ(X);
FOR I:= 1 TO L DO
WRITE (ELEMENT[P[I]],' ');
END;
(* MAIN ROUTINE *)
BEGIN
CREATE(0);
WHILE SEGMENT < LAST DO
BEGIN
SEGMENT:= SEGMENT + 1;
PROCSEG (0);
END;
REPORT(L);
END.
|
Listing 1.
HTML customization by
Werner Cirsovius
January 2015
© CL Publications
 Computer journals have recently published a number of articles on sorting algorithms.
The authors have usually favored the comparison method used in the Shell sort and in C.A.R.Hoare's Quicksort.
Some have noted as well ihe existence of the distribution or dispersion method, which also goes under the names of hash coding, address calculation, bulldozer sort, and range sorting.
Computer journals have recently published a number of articles on sorting algorithms.
The authors have usually favored the comparison method used in the Shell sort and in C.A.R.Hoare's Quicksort.
Some have noted as well ihe existence of the distribution or dispersion method, which also goes under the names of hash coding, address calculation, bulldozer sort, and range sorting.

