|
The following article was printed in June 1985 of the magazine „Computer Language".
|
A base article referring to binary trees and B-trees.
|
|
Binary trees and B-trees
By Namir Clement Shammas
|
 In the last two columns we discussed I hash-based searching for data resident in either RAM or storage disks.
In this issue we will examine alternative techniques, namely, those based on tree data structures.
In the last two columns we discussed I hash-based searching for data resident in either RAM or storage disks.
In this issue we will examine alternative techniques, namely, those based on tree data structures.
Efficient search methods that do not employ hashing must rely on having the data set up in some orderly fashion.
For example, seeking specific information in a list of items is less time consuming if the list is sorted.
Otherwise the entire list must be examined.
A sorted list can be maintained by performing an insertion sort with each new element added.
A secondary index list can be used to speed up the search.
It becomes apparent that as the list size grows, the average number of shifted list members increases.
Another way for maintaining data in sorted order, without the disadvantage of moving a lot of information, is to use binary trees.
Trees are nonlinear data structures where each element, called a node, may be connected to two or more other nodes.
A binary tree is one whose nodes are connected to two other nodes at most.
Thus it is a two-way tree having a left and right pointer.
The topmost node is also called the root.
This node is the first one added to the tree.
The nodes that point nowhere (have null pointers) are called terminal nodes or leaves.
How is data insertion carried out in a binary tree?
The very first inserted element becomes the root.
Every other data element is inserted following a recursive algorithm.
Step 1. The root is the first node used in the comparison step.
Step 2. The search key of the new data clement is compared with the node key.
If the search key is less than the node key, the node's left subtree branch is searched.
If not, the right subtree branch is searched.
Step 3. If either of the subtree branches is empty, then it becomes the location of the new key.
The insertion process terminates.
Otherwise it continues at the next step.
Step 4. The first node encountered in the left or right branches becomes the new comparison node.
The process is resumed at step 2.
Searching in a binary tree is conducted similarly.
The same comparison scheme is used until either a match to the search key is found somewhere or the search fails at a terminal node.
Deleting a node from a binary tree is not a simple operation.
The type of node deleted (root, nonterminal or terminal) decides the complexity involved.
Terminal nodes are the easiest to delete.
Other nodes will leave behind gaps to be filled, which is done by reorganizing the portion of the tree that was connected to the deleted node.
The worst case is when the root is deleted.
The right subtree nodes are rearranged.
The whole process looks like a power struggle in a dicatorship.
When a death occurs in the government, the lower ranked the deceased, the less disturbance there is in the land.
The reverse is also true, especially when the "head" (the root) of the country passes away.
In that case there is a power struggle among the next-in-rank players and their clans (corresponding to subtrees).
Binary trees allow for efficient searching and maintaining sorted lists kept in computer memory.
In languages like Pascal and Modula-2, nodes can be dynamically allocated and/or deallocated, creating trees in memory whose sizes are limited by hardware capacity.
Pointers are used to access nodes.
Dynamic trees spare the programmer from being locked in a predefined, fixed size array representing the nodes.
Recursive search methods allow for easier algorithms for the traversal of the tree.
Terminal nodes would cause an automatic backtracking to higher nodes.
All these advantages are lost when fixed arrays using nonrecursivc searches are employed.
Now the terminal nodes must be supplied with special pointers to guide the search resumption.
This kind of binary tree, is called threaded.
Binary trees may be used to store keys in memory (when a data maintainance session is in progress) while the complete records are stored on disk.
This allows for a faster RAM-based search and one-disk access. This scheme is feasible in the case of sufficient memory, and the search keys represent a small portion of the data records.
Maintaining a balanced binary tree is important for fast searching.
The insertion and deletion of keys occur in an unpredictable order.
This can very well lead to unevenly distributed branches.
The worst case is to have all the nodes in one subtree while the other is empty.
This creates a big linked list!
It happens when a perfectly sorted array is inserted in a binary tree.
The AVL trees (named in honor of two Soviet mathematicians, G.M. Adelson-Velskii and E.M. Landis, who described the balancing method) use algorithms that keep the binary trees in tune.
This is done first by assigning a balance factor to each node, reflecting the tilt in its subtrees.
There are three cases: tilted to the left, right, or balanced.
As new nodes are added and subtrees grow, there is a tendency to widen the difference in the heights of different subtrees.
The insertion algorithm incorporates code lines that deal with any imbalance as soon as it occurs (
Listing 1).
The action taken is to rotate subtrees either to the left or right to restore the balance.
As PPL code shows, there is a lot of node rearrangement done.
Deleting nodes from an AVL tree requires moving nodes around and adjusting subtrees to maintain the balance.
Since the AVL binary trees maintain balanced subtrees, one can use the following technique to increase the search speed in a large AVL tree.
The method will actually cause the tree structure, by academic definition, to cease being a true binary tree.
We can attach "zoom" pointers along the outer node edges in both left and right subtrees, starting with the root.
Each zoom pointer establishes a double-link between nodes and another that is n nodes downward.
The search begins with using the zoom pointers, which allows for faster traversal along the edges.
Every time a key comparison test fails, we use the next zoom pointer to locate the next node.
When the key comparison test fails or we reach the terminal nodes, we retreat to the last node searched.
We resume searching by examining neighboring nodes.
A variation of this scheme is to collect the zoom pointers in two separate lists or arrays, one for each primary subtree.
A comparison with the root key decides which list to use.
Instead of dealing with zoom pointers sequentially, we use the interval halving technique.
We first compare the search key with the node key of the median zoom pointer.
This decides which half of the list will be used in the next search. We select the median zoom pointer of the new half-list and so on.
 What about searching in data files?
How applicable arc binary tree techniques?
The answer is that basically there is nothing wrong with applying the preceding to data files, except for the slowness of the hardware.
Accessing data from a disk is much slower than accessing information from computer memory.
What about searching in data files?
How applicable arc binary tree techniques?
The answer is that basically there is nothing wrong with applying the preceding to data files, except for the slowness of the hardware.
Accessing data from a disk is much slower than accessing information from computer memory.
The solution is to read as many keys at a time and use them in multiway decision making.
Notice that we said keys and not records, because the former are usually much smaller than the latter.
This helps in having more dense information per unit storage.
Immediately we realize that we have expanded the concept of a binary or twoway tree into an m-way tree.
Instead of accessing single nodes from RAM, we read pages or buckets of keys or records.
Such trees are called B-trees (
Figure 1) after R.Bayer.
Like a binary tree, a B-tree has a root page or node (containing multiple keys).
The number of keys per page is also called the order of the B-tree.
The keys are arranged by insertion sorting to maintain the advantage of searching a sorted list.
Each key has a page pointer and a data record pointer associated with it.
To resume searching, the page pointer is used to point to the next page.
When a key matches a sought key, the data record pointer is used to access the entire record from the data file.
Terminal pages or nodes are called leaves.
Their data structure is identical to any other nodes.
B-trees, by definition, must follow certain structural rules and behavior.
While this may seem an imposed restriction, it actually gives the B-tree a sustained balance and fast search capability.
♦ All leaves are on the same level
♦ All nodes and leaves are at least half
full.
Donald Knuth has suggested that each page be two-thirds full. This type of tree is called the B* tree.
Listing 2 shows the PPL code for search routines in B-trees.
The next CrossThoughts column, which resumes the modified B-tree discussion, will present the PPL code for insertion.
It is very similar to that of B-trees.
The code presented is nonrecursive.
The search starts at the root page.
Procedure SearchNode is used to compare the search key with the page keys.
If a match is found, the search in the B-tree ends, and the appropriate data record pointer is used to access the information sought from the data records file.
Conversely, the comparison yields the pointer for the next page to be searched.
This takes us to the next page located one level lower than the current one.
This process repeats itself until the leaf pages are searched.
A search to insert keys in the B-tree is similar.
The existence of matching keys may flag an error if stored keys are to be unique.
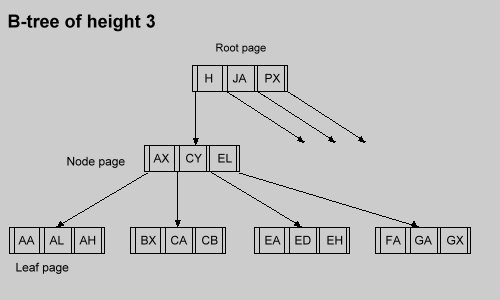
Figure 1.
 How do B-trees grow?
How are keys rearranged in the process?
The answer lies in the fact that their growth is very much affected by the structural rules mentioned earlier.
How do B-trees grow?
How are keys rearranged in the process?
The answer lies in the fact that their growth is very much affected by the structural rules mentioned earlier.
Initially there is one empty page.
As keys are added and fill out the page, the following takes place when attempting to add a key to a full page.
The page keys read in memory and the new key is inserted in the key list such that a perfect sorted order is maintained.
Next, the median key is selected, dividing the list into two halves.
The lower half is written back to the old page, while the upper half is written to a newly created page.
The median itself is stored in another, higher level, new page.
This makes the B-tree grow by one level.
The page containing the median key becomes the root page.
A comparison with the latter key will guide the search toward either leaf page.
This scenario takes place at the first growth stages of the B-tree.
As more keys are added, they are all inserted in the leaf pages.
As each leaf page becomes full, it is split into halves and the median key inserted into the parent node page.
If the latter becomes full, the same operation is carried out, resulting in two new, half-full nodes.
Their median is inserted or used to create a new parent page node.
The cascading effect is very evident when adding a new key to a B-tree filled at a certain height.
This yields a new root page and an increase in tree height.
Deleting keys from B-trees dictates that the remaining structure not violate the definition rules.
If this leaves a page less than half full, one of two things may occur.
If an adjacent page is more than half full, it will export a key to the key-deficient page.
Otherwise the two pages are combined.
This may affect the parent nodes and require additional adjustments.
While B-trees are very advantageous to use, they certainly have their drawbacks.
One of them is to search for a key and then read subsequent or previous keys, producing an ascending/descending sorted list.
This process involves a lot of jumping between pages with a relatively high number of I/O accesses.
Is there a solution to this problem?
Yes — it is called the B+ tree, the subject of our next column.
We will also discuss an additional modification for the B+ tree.
Binary trees have applications in subjects other than sorting and searching.
They can be used as parsing trees reflecting the order and priority of code execution, such as mathematical expressions.
This application will be discussed in a future column.
I look forward to hearing from you if you have any comments or thoughts to share about this column's subject.

AVL binary tree insertion routines
--------------------------------------------------------- AVL tree
EXPLICITLY RECURSIVE PROCEDURE Insert(VAR Root: Node_Pointer;
New_Rec : Node_Rec;
VAR IsTaller : BOOLEAN)
-- Inserting a new node in an AVL tree and keeping balanced tree
-- HasTallerSubtree is of type BOOLEAN
-- Balance_Factor is [-1..1] reflects the tilt of the tree
IF Root = nil
THEN Set Root to point to New_Rec
BalFactor = 0; IsTaller = TRUE
New_Rec.Left_Ptr = nil; New_Rec.Right_Ptr = nil
ELSE
IF New_Rec.Key <= Root^.Key
THEN
Insert(Root^.Left_Ptr,New_Rec,HasTallerSubtree)
IF HasTallerSubtree
THEN
CASE BalFactor OF
WHEN -1 => LeftBalance
WHEN 0 => BalFactor = -1; IsTaller = TRUE
WHEN 1 => BalFactor = 0; IsTaller = FALSE
END CASE
ELSE IsTaller = FALSE
END IF
ELSE
Insert(Root^.Right_Ptr,New_Rec,HasTallerSubtree)
IF HasTallerSubtree
THEN
CASE BalFactor OF
WHEN -1 => BalFactor = 0; IsTaller = FALSE
WHEN 0 => BalFactor = 1; IsTaller = TRUE
WHEN 1 => RightBalance
END CASE
ELSE IsTaller = FALSE
END IF
END IF
END IF
END Insert
PROCEDURE RightBalance
-- P1 and P2 are of type Node_Pointer
P1 = Root^.Right_Ptr
CASE P1^.BalFactor OF
WHEN 1 => Root^.BalFactor = 0; P1^.BalFactor = 0;
RotateLeft(Root); IsTaller = FALSE
WHEN -1 => P2 = P1^.Left_Ptr
CASE P2^.BalFactor OF
WHEN 0 => Root^.BalFactor = 0; P1^.BalFactor = 0
WHEN -1 => Root^.BalFactor = 0; P1^.BalFactor = 1
WHEN 1 => Root^.BalFactor = -1; P1^.BalFactor = 0
END CASE
P2^.BalFactor = 0; RotateRight(P1); RotateLeft(Root)
IsTaller = FALSE
WHEN OTHERWISE => -- do nothing
END CASE
RightBalance
PROCEDURE RotateLeft(VAR Ptr : Node_Pointer)
-- Tempo_Ptr is a local Node_Pointer
IF (Ptr = nil) OR (Ptr^.Right_Ptr = nil)
THEN DISPLAY "Error"
ELSE Tempo_Ptr = Ptr^.Right_Ptr; Ptr^.Right_Ptr = Tempo_Ptr^.Left_Ptr
Tempo_Ptr^.Left_Ptr = Ptr; Ptr = Tempo_Ptr
END IF
END RotateLeft
|
Listing 1.
|
B-tree searching routines
---------------------------------------------------------- B-tree
-- Data types involved are:
-- Node_Rec = RECORD
-- Count_Node_Key : INTEGER
-- Node Key : ARRAY[1..MAX] OF Key_Data
-- Node_Ptr, Data_Rec_Ptr : ARRAY[1..MAX] OF INTEGER
-- END RECORD
-- Variables used are:
-- Leaf : Leaf_Rec
-- Node : Node_Rec
-- ROOT, HEIGHT, MAX, MIN, NUM_PAGE : INTEGER
-- We assume that the "BTREE_Key_File" key file and "Record_File" data
-- file have been opened prior to any call.
PROCEDURE Search(Soughtkey : Key_Data
ROOT, HEIGHT : INTEGER
VAR Found : BOOLEAN
VAR SoughtLeaf, Sought_Loc : INTEGER
VAR Leaf : Leaf_rec)
-- Search procedure for B-tree
Found = FALSE
IF HEIGHT > 0 THEN
INITIALIZE: None
LOOP
BEGIN IF (HEIGHT <= 1) OR Found THEN EXIT END IF
READ BTREE_Key_File,ROOT,Node
SearchNode(SoughtKey,Node,Found Sought_Loc)
IF NOT Found THEN HEIGHT -= 1;
ROOT = Node.Node_Ptr[Sought_Loc]
END IF
END LOOP
TERMINATE:
IF Found AND search is in access mode THEN
READ Record_File,Node.Data_Rec_Ptr[Sought_Loc],Records
END IF
END IF
END Search
-------------------------------------------------------------------
PROCEDURE SearchNode(SoughtKey : Key_Data;
Node : Node_Rec;
VAR Found : BOOLEAN;
VAR Sought_Loc : INTEGER)
BEGIN
IF SoughtKey < Node.Node_Key[1]
THEN
Found = FALSE
Sought_Loc = 1
ELSE
INTIALIZE: Sought_Loc = Node.Count_Node_Key
LOOP
BEGIN IF (SoughtKey >= Node.Node_Key[Sought_Loc]) OR
(Sought Loc <= 1) THEN EXIT END IF
Sought Loc -= 1
END LOOP
TERMINATE: Found = (SoughtKey = Node.Node_Key[Sought_Loc])
END IF
END SearchNode
|
Listing 2.
|
HTML customization by
Werner Cirsovius
January 2015
© CL Publications
 In the last two columns we discussed I hash-based searching for data resident in either RAM or storage disks.
In this issue we will examine alternative techniques, namely, those based on tree data structures.
In the last two columns we discussed I hash-based searching for data resident in either RAM or storage disks.
In this issue we will examine alternative techniques, namely, those based on tree data structures.
 What about searching in data files?
How applicable arc binary tree techniques?
The answer is that basically there is nothing wrong with applying the preceding to data files, except for the slowness of the hardware.
Accessing data from a disk is much slower than accessing information from computer memory.
What about searching in data files?
How applicable arc binary tree techniques?
The answer is that basically there is nothing wrong with applying the preceding to data files, except for the slowness of the hardware.
Accessing data from a disk is much slower than accessing information from computer memory.

 How do B-trees grow?
How are keys rearranged in the process?
The answer lies in the fact that their growth is very much affected by the structural rules mentioned earlier.
How do B-trees grow?
How are keys rearranged in the process?
The answer lies in the fact that their growth is very much affected by the structural rules mentioned earlier.