Im Magazin „BYTE" wurde in der Ausgabe Oktober 1980 der folgende Artikel abgedruckt.
Ein grundlegender Artikel über die Binary Tree Sortierung. Er enthält Beispiele in BASIC und PASCAL

Sorting with Binary Trees

Bill Walker
University of Oklahoma
School of Electrical Engineering
and Computer Science
202 W Boyd
Normian OK 73019
Of the numerous sorting techniques know to the average computer user, one that is seldom talked about is the binary sort. This is probably because, at first glance, it seems unnecessarlly complicated when compared to, say, the common bubble sort. (The bubble sort is so-called because a new element reaching its proper position in a sorted list does so by being compared successively with each element already in the list, rising like a bubble from the bottom of the list.) Nonetheless, I was curious enough about the binary sort to compare it to the more common bubble sort in a practical demonstration. The results were interesting enough to warrant further study. First, let me describe the experiment.
The program of listing 1 (with line 5 deleted) was used to implement a binary sort on an 8 K Commodore PET. Timing comparisons were made, using the PET's internal real-time clock, for both this program and a bubble-sort program (not listed in this article), both of which were instructed to sort a random list of 100 integers. The binary sort took approximately half as long as the bubble sort to order the random list of numbers. However, the real payoff came when the computer was told to either add to or delete from the list, and then print the new sorted list. The bubble sort took the same amount of time it took to do its first sort, but the binary sort was finished before the display had time to record the fact.
It is on this seemingly amazing note that we begin a discussion of binary sorts.
Figures 1 and 2 are examples of what are called trees. They are extremely useful in several branches of mathematics and figure largely in the construction of a binary search. Trees are made of nodes (the circles in figures 1 and 2), each of which usually contains information. The single node in the top row is called the root. A given node can be connected to one or more nodes on the next level below it; if this is the case, the higher node is called the parent node (or parent), and the lower nodes directly connected to it are called its children.
Figure 1: A generalized tree. A tree is characterized by having only one root node (the one at the top) and hy each node (represented here as a circle) having zero or more nodes connected to it by a straight line. The nodes below the given node connected directly by one line segment are called child nodes; the node itself is called the parent node.
Figure 2: A binary tree. This tree is characterized by the properties that a given parent node can have, at most, two child nodes, and that each non-root node has exactly one parent. The child nodes are called the left child node and the right child node.
For years, mathematicians have known many properties of tree diagrams. Most of these properties are complex or so general as to be of little practical use. But if we restrict ourselves to a specific subset of trees with a given structure, these properties become readily understandable and usable. Figure 1 shows a general tree; figure 2 is an example of the type of tree that we will be studying, a binary tree.
Figure 3: A simple binary tree. Data is arranged within a binary tree so that the sequence right child, parent, left child gives the contents of the tree in sorted order. Here, the sorted order is 12, 15, 25.
Figure 4: Adding to a binary tree. The colored arrow shows the direction of search when placing a new node in a binary tree. Here, 14 is greater than 12, so it is ptaced as a right child of 12. Here, the sorted order is 12, 14, 15, 25.
Figure 5: Example of a binary tree. Here, more nodes have been added, giving the sequence 10, 12, 14, 15, 20, 25, 26.
Figure 6: Example of a binary tree. Here (6a), the binary tree of figure 5 is reproduced with numbers above each node that give the order in which the nodes were added to the tree. The table below (6b) gives the node number, key, left pointer, and right pointer of each node; both pointers refer to the node number of a node, not its key value. The ward NIL indicates there is no node in the direction given by the pointer.
A binary tree is characterized by the restriction that each parent node can have, at most, two children, and that any node (except for the root node) must have exactly one parent node. Later we will see that this kind of tree is well suited to representation in a digital computer, where the binary nature of decisions (answered with yes or no) goes hand in band with the maximum of two child nodes allowed each parent node.
How does this structure enable us to perform searches and sorts? If we define less than as meaning to the left and down and greater than as meaning to the right and down, this gives us an ordering that can be used to store members of a sorted list as nodes of a binary tree.
Suppose we start with three numbers: 15, 12, and 25. Since 15 is the first number encountered, we will designate it as the root of our tree. Since 12 is the next number in the list, we attach it below and to the left of the root node (12 is less than 15). Since the next number, 25, is greater than the root, 15, we attach it below and to the right of the root. This gives us the binary tree in figure 3.
Now let us add a new number to the list: 14. We can add this to the existing binary tree as follows: start at the root node, 15, and move to the left because the node we want to insert, 14, is less than 15. At the node numbered 12, we compare 12 to 14 and conclude that we should go to the right. Since no node exists to the right of 12, we can place a new node there with the value of the number to be added, giving us the binary graph in figure 4. Similarly, we can add the numbers 26, 20, and 10 to our tree, giving us the tree in figure 5.
Given the tree in figure 5 as a "sorted" tree, this implies that there is some procedure that allows us to extract the sorted list of numbers frorn the "sorted" binary tree.
If we were presented with the diagram of figure 3 and asked to read it in proper order, we would do so by first reading the leftmost node, then the parent, then the rightmost node. We note that the far more complicated trees of figure 4 and figure 5 can be read in a similar fashion by first visiting the lef tmost node in each branch, then moving to the parent, then to the rightmost node, then moving to the next group and repeating the sequence.
Unfortunately, such a description, while easy for people, is tough for computers, because computers lack the ability to observe spatial placement of nodes. It becomes necessary for us to provide the computer with a series of pointers that indicate the relationships between nodes. Each node is provided with two pointers, one of which points to the lef t child of the node, while the other points to the right child of the node.
In figure 6, we have listed the nodes (in the order encountered) and the left and right pointers of each parent node. Note the presence of the word "NIL" for the four children at the bottom of the branches. These represent pointers to possible future nodes that have not yet been added to the tree.
To properly pass through the computer representation of the tree, we have to supply it with the proper information as to the relationship of the nodes to each other. This can be done economically by assigning four numbers to each node, as shown in figure 7. The four numbers are the number of the node, the value or key of the node, and the left and right pointers to the node numbers (not to their keys).
Some explanation should be given of the values that can be assumed by the left and right pointers. The left pointer always points to either a node number (greater than zero) or zero (denoting the end of one "branch" of the tree in the leftward direction).
The right pointer can assume either positive or zero values with the same meanings as above. In addition, it can be negative; this is an upward pointer to the node that is the next node in the ascending key sequence. (The node with the upward pointer is the rightmost node of a left subtree; the node being pointed to is the parent node of this same left subtree.) An example of this in figure 7 is the upward pointer from node 4 to node 1; the upward pointer denotes that the subtree of nodes 2, 4, and 7 has been listed already.
Figure 7: Computer representation of a binary tree. In the BASIC program of listing 1, each node is represented by four numbers: the node number (given for purposes of illustration only), the key, and the right and left pointers. To "thread" the tree so that a thread of pointers runs through the nodes in their sorted-key order, a right pointer, when negative, points not to a right child node but to the ancestor node that follows the current node in the sorted sequence; these upward right pointers are drawn in color.
Listing 1: BASIC program for sorting a threaded binary tree. This program allows the user to create, add to, delete from, and list a binary tree. The tree is threaded in that it is possible to print the tree sorted in ascending key sequence by using the pointers associated with each node. This version is written in Microsoft BASIC and currently runs an an Apple II. With the deletion of line 5, it has also been run an the Commodore PET, the Radio Shack TRS-80, and a PDP-10. It should also run without modification on any other computer using Microsoft BASIC. [Listing]
Listing 2: Running the program of listing 1. In this listing, a hundred random numbers are generated, used to create a binary tree, and listed in sorted key sequence. The node containing key value of 8 is deleted, a node with key value of 39 is added, and the tree is listed again.
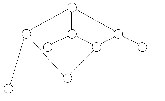
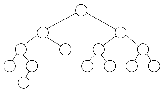
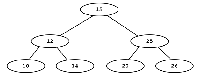
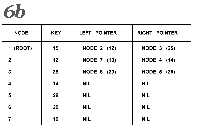
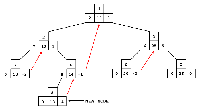
The upward pointers in figures 7 and 8 are highlighted for clarity. Note that only one node in the tree, the rightmost node (containing the largest erttry in the sorted list), has a right pointer with a value of zero. This is a signal that the end of the tree has been reached.
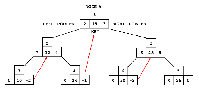
Let us look at the process of reading the sorted numbers from the tree in figure 7. We enter the tree at the root node, which contains the integer 15. We move ieft down the tree until we encounter the first node with a Ieft pointer of zero (which we will also refer to as NIL). This is node number 7, the one that contains 10 as its key. We print the value 10 and follow the right pointer back up the tree to node 2, which contains a 12. We print the 12 and follow the right pointer of this node to node 4.
Figure 8: Addition of a node to a binary tree. Using the notation of figure 7, this figure shows the addition of node 8, which has a key value of 13. The Ieft pointer of node 8 is 0, denoting no Ieft child. The right pointer of node 8 is -4, denoting two things: first, that node 8 has no right child; and second, that the node whose key follows the key of node 8 in the sorted-key sequence is node 4. The upward right pointers are shown here in cotor.
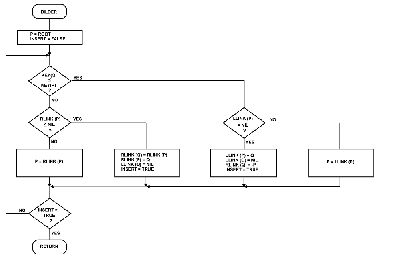
Figure 9: Flowchart for subroutine FIX. This subroutine initializes storage space in a Computer for later use as a threaded binary tree.
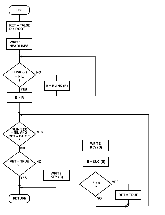
Figure 10: Flowchart for subroutine BILDER. This subroutine adds node Q (with key value KEY (Q)) to the existing binary tree.
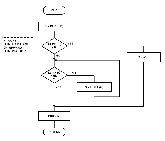
Figure 11: Flowchart for subroutine SEARCH. This subroutine searches the binary tree for a node with a key value of ALPHA.
Node 4 has no left child, therefore we print 14 and follow the right pointer back up the tree to node 1. At node 1, we print 15 and follow the right pointer to node 3. Node 3 has a left child, so we move from node 3 along the left pointer to node 6. Node 6 has no left child, so we print the contents of node 6, which is 20.
Following the right pointer of node 6 back to node 3, we print its value, 25. Following the right pointer of node 3 to node 5, we find the 26, which has no left child. So we print 26 and look at the right pointer of this node. Since the right pointer is NIL, the rightmost node must have no sucessor. This means it is the last node in the tree, so we end the sort.
This is certainly a lot of trouble--unless you want to do more than just sort your numbers once. And it is here that the binary tree shows its greatest advantage. In most sort procedures, if you add a number to the list to be sorted, you have to completely re-sort the new list. But with a binary tree, all you have to do is add one node and list the tree (both of which take much less time than a complete re-sort).
Figure 8 shows the addition of one node, a 13, to be added to the tree of figure 7. The 13, being the eighth number in our list, becomes node 8. It is added to the tree at the bottom of the appropriate branch, necessitating the change of only one pointer in the old tree: the left pointer of node 4 now points to node 8. All the other pointers remain intact, thus keeping computer time to a minimum. Best of all, no key values of nodes have been altered in the least.
Deletion of nodes from the tree is not as obvious a procedure as one might suppose.
It is not hard to write a subroutine that will traverse a binary tree in the proper order. Nor is it difficult to write a subroutine to add a node to a tree--or, equivalently to add a number to a sorted list. Deletion of nodes from the tree, however, is not as obvious a procedure as one might suppose.
Detaching the node to be deleted is simply a matter of destroying the pointers from other nodes to the undesired node. But repair of the tree diagram--connecting nodes below the deleted node to the body of the tree--is not quite so easy. There are several cases to be considered, all of which are handled by the subroutine DEL.
The binary-tree-sort program in listing 1 was designed as a main routine and a collection of subroutines. A brief description of each subroutine (given below) and a flowchart describe the operation of each of the subroutine modules. Each of the subroutines was written in structured fashion. Although the main routine is also structured, the current listing reflects a certain amount of modification and experimentation; in other words, it has not been rewritten for optimal structure.
Figure 12: Flowchart for subroutine LIST. This subroutine traverses the binary tree in sorted key order and prints the nodes as they are encountered.
Figure 13: Flowchart for subroutine SUC. This subroutine, given for a node P, finds the number of the node that is the successor of node P in the sorted-key sequence.
The main routine of listing 1 contains the following sequence: an array of 100 random integers is created and used to create a sorted binary tree; the binary tree is listed; then the user is given the options of adding to the tree, listing the tree, or deleting from the tree. All the necessary subroutines are included in this listing.
This program was originially written in FORTRAN and was later translated to BASIC, running first on a PET, then on an Apple II. The program contains some redundancies so that the program will run as written on both machines; the only restriction is that line 5 must be deleted before running the program on the PET. The structured programming techniques used in writing the original FORTRAN version proved to be quite necessary when translating and debugging the BASIC version. I feel that structured programming techniques are essential to a program of any size.

Subroutine Descriptions

FIX: The purpose of the subroutine FIX (see flowchart in figure 9) is to initialize all the space to be used for tree nodes before the binary tree is built. The FIX subroutine must be presented with N, the maximum number of nodes to be available to the tree. Once the tree has N nodes, there are no provisions in this program to make additional space available.
BILDER: Subroutine BILDER adds a new data entry to the binary tree, placing it in correct relation to the other nodes in the tree. Within the BILDER routine, the node to be added is numbered Q and has a value of KEY(Q). The algorithm (see flowchart in figure 10) compares the node to be added, Q, with other nodes (starting with the root node and moving down the tree) until it can be placed in proper relation to a parent node (a node that has a NIL pointer pointing to where node Q should go).
SEARCH: The SEARCH subroutine (see figure 11) returns the node number of a key with value ALPHA. The node number (or zero if the node is not found) is returned in the variable SEARCH. The search done is not a linear search but rather a binary search like the one used in BILDER. A binary search is named such because each decision halves the area to be searched.
LIST: The LIST subroutine (see figure 12) lists the nodes of the tree in ascending key sequence by traversing the tree from its leftmost to its rightrnost node. LIST follows an optimal path down the leftmost branch of the tree until it encounters a node the left pointer of which has value NIL; this node contains the smallest key value. Having found the smallest key value, LIST then calls SUC (the successor subroutine) repeatedly to find successor nodes; key values are printed in the order they are encountered. When a node is found that has a right pointer of value NIL, the node with the highest key value has been found, and the LIST subroutine has finished.
Figure 14: Flowchart for subroutine PAR. This subroutine finds the parent node of a given node P.
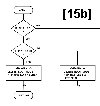
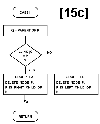
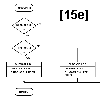
Figure 15: Flowchart for subroutine DEL. Figures 15a thru 15e describe the algarithm, with further description given in table 1. Case I is executed when the node to be deleted, P, is the root node. Case II, group A is executed when the node to be deleted, P, is the left child of a parent node. Case II, group B is executed when the node to be deleted, P, is the right child of a parent node. 
Case I: Node P to be deleted is the root node.
  Subcase A: Node P has no children.
      1. Set EMPTY = TRUE.
      2. Set N (the number of nodes in the tree) to zero.
  Subcase B: Node P has only a right child.
      1. Set new root equal to right link of old root.
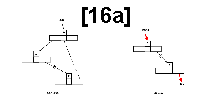
  Subcase C: Node P has only a left child (see figure 16a).
      1. Set new root equal to the left link of the old root.
      2. Search right branch of left child of P for its
         rightmost node R. Set the right pointer of R to NIL.
  Subcase D: Node P has a left and a right child (see figure 16b).
      1. Set new root equal to the right link of old root.
      2. Search left branch of right child of P for its
         leftmost node S. (S will have a left pointer of NIL.)
         Set left pointer of S to the left child of the
         old root (that is, to point to the left subtree
         of the old graph).
      3. Search right branch of left child of P for its rightmost
         node R. Set right pointer of R to point to S.

Case II: Node P to be deleted is not the root node.
  Group A: Node P is the left child of parent node Q.
   Subcase 1: Node P has no children,
       a. Set LEFT link of parent Q to NIL.
   Subcase 2: Node P has only a right child.
       a. Set LEFT pointer of parent node Q to right child of P.
   Subcase 3: Node P has only a left child (see figure 16c).
       a. Set LEFT pointer of parent node Q to left child of P.
       b. Search right branch of left child of P for its
          rightmost node R; this node will have an upward right
          pointer to P. Assign the right pointer of R the value of
          the right pointer of P.
   Subcase 4: Node P has a left and a right child (see figure 16d).
       a. Set LEFT pointer of parent node Q to right child of P.
       b. Search left branch of right child of P for its
          leftmost node S. (S will have a left pointer of NIL.)
          Assign the left pointer of S the value of the left pointer
          of P.
       c. Search right branch of left child of P for its
          rightmost node R. Assign the right pointer of R the
          value -S.
  Group B: Node P is the right child of parent node Q.
   (Subcases 1 thru 4 are the sarne if the word RIGHT is
   substituted for the capitalized word LEFT in each subcase.)

Table 1: Analysis of node deletion in a threaded binary tree. This table details the operations necessary to delete a node, labeled P, from a threaded binary tree. This table is associated with figure 15, figure 16, and listing 1.
SUC: The SUC subroutine, shown in figure 13, when given the node numbered P, returns the value SUC, which is the number of the node that follows node P in the ascending key sequence. If the right pointer of P, named Q, is an upward pointer (value less than zero), the absolute value of the pointer is the successor node. If Q is a downward pointer, the leftmost child of Q is the successor node. A SUC value of NIL is returned if node P is the rightmost node in the tree.
PAR: The PAR subroutine, shown in figure 14, returns in variable PAR the number of the parent node of node P. (Remember that every node in a binary tree except the root node has exactly one parent node.) As in BILDER and LIST, a binary search starting at the root uses the values of the current node key and the key of node P to guide the search down the tree until the parent of P is found. This method is much faster than linearly traversing the tree using the SUC subroutine.
DEL: The DEL subroutine to delete a node from the tree is the most complicated of the subroutines presented. This is due largely to the necessity of reestablishing the thread that runs through the tree. The algorithm for node deletion is given in figure 15 and table 1; the examples in figure 16 are referred to by table 1.
Figure 16: Examples of node deletion. Figures 16a thru 16d ate used to illustrate the structure of a binary tree before and after the deletion of node P; they are referred to by table 1. A broken arrow (for example, A to R) denotes an eventual connection through zero or more intermediate children. A dashed arrow denotes an upward right pointer to the next node in the sorted key sequence. A gray arrow in the "after" drawing denotes a pointer that hos been changed by the deletion.

A Pascal Implementation

A second and somewhat different version of the binary tree program is given in listing 3. This version does not use a threaded tree (ie: there are no upward right pointers). Because of this, the subroutine to add a node is almost trivial, and the delete routine is greatly simplified. This implementation is, in general, altogether nicer.
Listing 3: Pascal program for sorting a binary tree. Due to the nature of the program, the binary tree does not need to be threaded; this simplifies most of the procedures and functions of the program. Program details are given in the text. This program, written to run on a Digital Equipment Corporation PDP-11/70, should run in UCSD Pascal without modification. [Listing]
The main change in this listing (compared to the BASIC program of listing 1) is the use of the scan procedure to traverse and list the tree. The scan procedure uses a stack, which is maintained by the initstack and push procedures, along with the pop function. The scan algorithm is as follows:
1) Move left along the branches of the tree, placing each node traversed onto the stack.
2) When a left pointer of NIL is reached, pop the stack and print what was just popped.
3) If you can, move right one node and go to step 1; otherwise, pop the stack, print the node popped, and repeat step 3.
4) Underflow of the stack represents the end of the algorithm.

Due to the nature of the Pascal language, the listing itself serves to document the algorithm. In all fairness to BASIC, it must be stated that the Pascal program of listing 3 is simpler partially due to the absence of the thread running through the binary tree.

Acknowledgements

I would like to thank the Computer Corner of Amarillo, Texas, for the use of their printer to produce listings 1 and 2.

Eingescanned von Werner Cirsovius
April 2012
© BYTE Publications Inc.