Im Magazin „Dr. Dobb's Journal of Computer & Orthodontia" wurde in der Nummer 30 (Jahr unbekannt) der folgende Artikel abgedruckt. Ich habe den Artikel hier übersetzt

Dieser sehr gute Artikel befasst sich auf praktische Weise mit einem Sortierproblem, wie man es beim Arbeiten mit Symbolen findet.

Binary Tree Manipulation on the 8080

BY MIKE GABRIELSON
Box 2692
Stanford, Calif. 94305

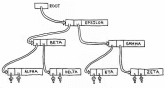
Imagine that we are writing a compiler. How should the symbol table be organized? One possibility is to use a binary tree. Figure 1 illustrates a binary tree that contains seven symbols (strings representing variable names).

Figure 1. A Binary Tree

Each symbol is contained in a node along with two pointers. The pointers are used to link together the nodes of the tree. A special pointer called the root points to the topmost node of the tree. (Computer trees grow upside down.) Grounded pointers on the bottommost nodes have nothing to point to.

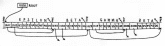
On the 8080 and similar computers, we can let each pointer be a 16 bit address, and each symbol can be an ASCII string. Figure 2 shows a portion of our tree as it might actually be stored in an arbitrary region of memory.

Figure 2. The Tree Stored in Memory

By convention, we will set grounded pointers to a zero value, and delimit each string with the NUL character. An actual symbol table for a compiler would include some extra bytes in each node for flags, values, and other information about each symbol, but we'll ignore that to simplify the examples.

The symbols in our tree are arranged in a special way: if we pick any node, we find that the left pointer (if not grounded) points to a subtree containing symbols all alphabetically less than (preceding) the symbol in the node. Similarly, the right pointer points to a subtree containing symbols all alphabetically greater than (following) the symbol in the node. Maintaining the tree in this ordered manner allows us to design very simple but effective algorithms to manipulate the data in the tree. For example, suppose our compileer needs to look for a symbol in the tree. How should the tree be searched? Starting with the first node (pointed to by the root), we compare the node's symbol to the symbol we desire. If there's a match, we're done. If our symbol is less than the node's symbol, we follow the node's left pointer and repeat the test with that node. If our symbol is greater, we pick the right subtree, and so on down the branches until we find a match or until we reach a grounded pointer, which indicates the symbol is nowhere in the tree. The sample subroutine called SEARCH will search a binary tree like ours using this algorithm.

Subroutine called SEARCH:
1 ; SEARCH - search symbol tree for an ASCII string 2 ; Mike Gabrielson 8/10/78 3 ; accepts: BC = address of string to look for, terminated by NUL 4 ; DE = address of ROOT pointer 5 ; HL = contents of ROOT pointer (equal to address of 6 ; first node if not grounded) 7 ; returns: carry set if string not found in tree (DE = address 8 ; of last grounded pointer) 9 ; else carry cleared (string found, HL = address of 10 ; node containing the matching string) 11 ;=============================================================== 12 13 NUL = 0 ;end of string character 14 15 0000 7C SEARCH: MOV A,H ;is the pointer grounded, 16 0001 B5 ORA L ;indicating end of tree? 17 0002 37 STC ;(assume "yes") 18 0003 C8 RZ ;yes, end of tree, string not found 19 0004 C5 PUSH B ;no, save address of caller's string 20 0005 E5 PUSH H ;save address of node 21 0006 23 INX H ;skip past the node's 22 0007 23 INX H ;left and right subtree pointers 23 0008 23 INX H ;and stop at the first character 24 0009 23 INX H ;of the node's string 25 000A 0A NEXTC: LDAX B ;get character from caller's string. 26 000B BE CMP M ;same as character in node's string? 27 000C C21600 JNZ TESTED ;no, wrong node 28 000F 03 INX B ;yes, 29 0010 23 INX H ;point to next character pair 30 0011 FE00 CPI NUL ;was that the end of the strings? 31 0013 C20A00 JNZ NEXTC ;no, test next pair 32 0016 E1 TESTED: POP H ;restore address of node 33 0017 C1 POP B ;restore address of caller's string 34 0018 C8 RZ ;done if strings matched (carry's cleared) 35 0019 DA1E00 JC LEFT ;pick left subtree if caller's string is low 36 001C 23 INX H ;else get address of right subtree pointer 37 001D 23 INX H 38 001E 56 LEFT: MOV D,M ;get address of subtree into DE 39 001F 23 INX H 40 0020 5E MOV E,M 41 0021 EB XCHG ;then into HL 42 0022 1B DCX D ;leave DE pointing to last node accessed 43 0023 C30000 JMP SEARCH ;continue searching down the tree
[Listing]

Subroutine called SEARCH:

1		; SEARCH - search symbol tree for an ASCII string
2		; Mike Gabrielson   8/10/78
3		; accepts: BC = address of string to look for, terminated by NUL
4		;          DE = address of ROOT pointer
5		;          HL = contents of ROOT pointer (equal to address of
6		;               first node if not grounded)
7		; returns: carry set if string not found in tree (DE = address
8		;               of last grounded pointer)
9		;          else carry cleared (string found, HL = address of
10		;               node containing the matching string)
11		;===============================================================
12
13			NUL = 0     ;end of string character
14	
15 0000 7C	SEARCH: MOV  A,H    ;is the pointer grounded,
16 0001 B5		ORA  L      ;indicating end of tree?
17 0002 37		STC         ;(assume "yes")
18 0003 C8		RZ          ;yes, end of tree, string not found
19 0004 C5		PUSH B      ;no, save address of caller's string
20 0005 E5		PUSH H      ;save address of node
21 0006 23		INX  H      ;skip past the node's
22 0007 23  		INX  H      ;left and right subtree pointers
23 0008 23		INX  H      ;and stop at the first character
24 0009 23		INX  H      ;of the node's string
25 000A 0A	NEXTC:	LDAX B      ;get character from caller's string.
26 000B BE		CMP  M      ;same as character in node's string?
27 000C C21600		JNZ  TESTED ;no, wrong node
28 000F 03		INX  B      ;yes,
29 0010 23		INX  H      ;point to next character pair
30 0011 FE00		CPI  NUL    ;was that the end of the strings?
31 0013 C20A00		JNZ  NEXTC  ;no, test next pair
32 0016 E1	TESTED:	POP  H      ;restore address of node
33 0017 C1		POP  B      ;restore address of caller's string
34 0018 C8		RZ          ;done if strings matched (carry's cleared)
35 0019 DA1E00		JC   LEFT   ;pick left subtree if caller's string is low
36 001C 23		INX  H      ;else get address of right subtree pointer
37 001D 23		INX  H
38 001E 56	LEFT:	MOV  D,M    ;get address of subtree into DE
39 001F 23		INX  H
40 0020 5E		MOV  E,M
41 0021 EB		XCHG        ;then into HL
42 0022 1B		DCX  D      ;leave DE pointing to last node accessed
43 0023 C30000		JMP  SEARCH ;continue searching down the tree

[Listing]

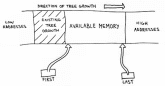
How do we grow a tree in the first place? One necessary ingredient to grow a tree is memory. Let's assume we have access to two new pointers. One pointer is called FIRST and is the address of the first byte of a contiguous chunk of memory available for the tree. The last available byte in the chunk is pointed to by LAST. This arrangement is illustrated in Figure 3.

Figure 3. Memory Allocation

Each time our tree needs a byte to grow, it can grab the byte pointed to by FIRST, and then increment FIRST. Memory is exhausted when FIRST passes LAST. Now we can modify our search so that when a symbol is not found in the tree, a new node is automatically grown for it. The next listing is a subroutine called LOOKUP which appends new symbols to the tree as necessary. (To simplify the code, this version of LOOKUP does not check if FIRST passes LAST, indicating memory overflow.) An example of a call to LOOKUP is

	LXI	B,STRING	;get address of string
	LXI	H,ROOT		;get address of ROOT
	MOV	D,M		;get contents of ROOT
	INX	H
	MOV	E,M
	DCX	H		;restore address of ROOT
	XCHG			;adjust registers for LOOKUP
	CALL	LOOKUP

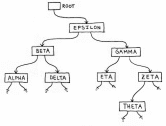
The calling sequence can be simplified if the contents of the 16-bit root and node pointers are maintained in standard Intel byte-reversed format, instead of unreversed as the code currently requires. Changing the code so that all pointers are byte-reversed is an easy exercise left to the reader. Figure 4 shows how the tree has grown after a LOOKUP of the symbol THETA.

Figure 4. New Growth

Subroutine called LOOKUP:
1 ; LOOKUP - find ASCII string in symbol tree 2 ; Mike Gabrielson 8/10/78 3 ; accepts: BC = address of string to look for, terminated by NUL 4 ; DE = address of ROOT pointer 5 ; HL = contents of ROOT pointer (equals address of 6 ; first node if not grounded) 7 ; returns: HL = address of tree node containing the string 8 ; carry set if a new node had to be grown 9 ; else carry cleared (symbol already in tree) 10 ; MEMORY OVERFLOW IS NOT TESTED FOR! 11 ;=============================================================== 12 13 NUL = 0 ;end of string character 14 15 !EXTRN SEARCH ;SEARCH is not defined in this assembly 16 !EXTRN FIRST ;external pointer containing address of 17 ;first byte of available memory for 18 ;growing new nodes 19 20 0000 CD---- LOOKUP: CALL SEARCH ;Symbol already in tree? 21 0003 D0 RNC ;yes, all done 22 0004 2A---- LHLD FIRST ;no, get address of node about to sprout 23 0007 E5 PUSH H ;save address of new node for return 24 0008 EB XCHG ;HL := address of last pointer SEARCHed 25 0009 72 MOV M,D ;replace grounded pointer with address 26 000A 23 INX H ;of new node 27 000B 73 MOV M,E 28 000C AF XRA A ;clear register A 29 000D 12 STAX D ;and ground the two subtree pointers in the 30 000E 13 INX D ;new node 31 000F 12 STAX D 32 0010 13 INX D 33 0011 12 STAX D 34 0012 13 INX D 35 0013 12 STAX D 36 0014 13 INX D 37 0015 0A SAVNAM: LDAX B ;get next character from caller's string 38 0016 12 STAX D ;save in new node 39 0017 03 INX B ;adjust pointers for next character 40 0018 13 INX D 41 0019 FE00 CPI NUL ;was that the end of the string? 42 001B C21500 JNZ SAVNAM ;no 43 001E EB XCHG ;get address of next available byte into HL 44 001F 22---- SHLD FIRST ;save new FIRST 45 0022 E1 POP H ;yes, restore address of new node 46 0023 37 STC ;indicate new node was grown for caller 47 0024 C9 RET
[Listing]

Subroutine called LOOKUP:

1		; LOOKUP - find ASCII string in symbol tree
2		; Mike Gabrielson   8/10/78
3		; accepts: BC = address of string to look for, terminated by NUL
4		;          DE = address of ROOT pointer
5		;          HL = contents of ROOT pointer (equals address of
6		;		first node if not grounded)
7		; returns: HL = address of tree node containing the string
8		;          carry set if a new node had to be grown
9		;          else carry cleared (symbol already in tree)
10		; MEMORY OVERFLOW IS NOT TESTED FOR!
11		;===============================================================
12
13			NUL = 0       ;end of string character
14
15			!EXTRN SEARCH ;SEARCH is not defined in this assembly
16			!EXTRN FIRST  ;external pointer containing address of
17				      ;first byte of available memory for
18				      ;growing new nodes
19
20 0000 CD----	LOOKUP: CALL SEARCH ;Symbol already in tree?
21 0003 D0		RNC         ;yes, all done
22 0004 2A----		LHLD FIRST  ;no, get address of node about to sprout
23 0007 E5		PUSH H      ;save address of new node for return
24 0008 EB		XCHG        ;HL := address of last pointer SEARCHed
25 0009 72		MOV  M,D    ;replace grounded pointer with address
26 000A 23		INX  H      ;of new node
27 000B 73		MOV  M,E
28 000C AF		XRA  A      ;clear register A
29 000D 12  		STAX D      ;and ground the two subtree pointers in the
30 000E 13		INX  D      ;new node
31 000F 12		STAX D
32 0010 13		INX  D
33 0011 12		STAX D
34 0012 13		INX  D
35 0013 12		STAX D
36 0014 13		INX  D
37 0015 0A	SAVNAM: LDAX B      ;get next character from caller's string
38 0016 12		STAX D      ;save in new node
39 0017 03		INX  B      ;adjust pointers for next character
40 0018 13		INX  D
41 0019 FE00		CPI  NUL    ;was that the end of the string?
42 001B C21500		JNZ  SAVNAM ;no
43 001E EB		XCHG        ;get address of next available byte into HL
44 001F 22----		SHLD FIRST  ;save new FIRST
45 0022 E1		POP  H      ;yes, restore address of new node
46 0023 37		STC         ;indicate new node was grown for caller
47 0024 C9		RET

[Listing]

A nice feature for our compiler would be the capability of listing the symbol table in alphabetical order. How can we list our tree? Because of the way the tree is ordered, one elegant algorithm we can use works as follows: before listing any node, first list the node (subtree, if any) pointed to on the left, then list the original node, then list the node (subtree) pointed to on the right. Start with the node pointed to by the root, but always try to first visit the left subtree at each node.

This is a recursive algorithm that is easy to implement on machines with a stack like the 8080. The final sample program is a recursive routine called PUTREE that will dump our tree using this algorithm. An example of a call ta PUTREE is

	LHLD	ROOT	;get contents of ROOT
	MOV	A,H	;swap H and L
	MOV	H,L	;to be consistent with 
	MOV	L,A	;rest of tree
	ORA	H	;is root grounded?
	CNZ	PUTREE	;no, output tree

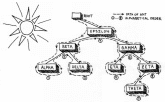
A way to visualize what's happening is to imagine an ant visiting each node by crawling around the edges of the tree (see Figure 5).

Figure 5. Tree Traversal

If the sun is shining from the upper left, and the ant shouts out each symbol the first time it crawls along a shaded side of the symbol's node, then the symbols will be shouted out in alphabetical order.

Subroutine called PUTREE:
1 ; PUTREE - Output symbol tree in alphabetical order 2 ; Mike Gabrielson 8/10/78 3 ; accepts: HL = contents of ROOT pointer (must not be grounded) 4 ; ============================================================= 5 6 !EXTRN PUTNAM ;this is an external routine not 7 ;defined in this assembly. PUTNAM 8 ;outputs the ASCII string addressed 9 ;by HL (which must be saved) and 10 ;terminated by NUL. 11 12 0000 D5 PUTREE: PUSH D ;save pointer to the pointer when reentered 13 0001 E5 PUSH H ;save address of node 14 0002 56 MOV D,M ;get pointer to left subtree into DE 15 0003 23 INX H 16 0004 5E MOV E,M 17 0005 23 INX H 18 0006 EB XCHG ;then into HL 19 0007 7C MOV A,H ;no left subtree? 20 0008 B5 ORA L ;(pointer grounded?) 21 0009 C40000 CNZ PUTREE ;subtree exists, traverse it now 22 000C EB XCHG ;restore address of original node to HL 23 000D 23 INX H ;skip right subtree pointer 24 000E 23 INX H ;and get address of symbol narae 25 000F CD---- CALL PUTNAM ;output the ASCII string 26 0012 2B DCX H ;get node's right subtree pointer into DE 27 0013 5E MOV E,M 28 0014 2B DCX H 29 0015 56 MOV D,M 30 0016 EB XCHG ;then into HL 31 0017 7C MOV A,H ;no right subtree? 32 0018 B5 ORA L ;(pointer grounded?) 33 0019 C40000 CNZ PUTREE ;subtree exists, traverse it now 34 001C E1 POP H ;restore stack 35 001D D1 POP D 36 001E C9 RET
[Listing]

Subroutine called PUTREE:

1		; PUTREE - Output symbol tree in alphabetical order
2		; Mike Gabrielson   8/10/78
3		; accepts: HL = contents of ROOT pointer (must not be grounded)
4		; =============================================================
5
6			!EXTRN PUTNAM ;this is an external routine not
7				      ;defined in this assembly.  PUTNAM
8				      ;outputs the ASCII string addressed
9				      ;by HL (which must be saved) and 
10				      ;terminated by NUL.
11
12 0000	D5	PUTREE:	PUSH D      ;save pointer to the pointer when reentered
13 0001	E5		PUSH H	    ;save address of node
14 0002	56		MOV  D,M    ;get pointer to left subtree into DE
15 0003	23		INX  H
16 0004	5E		MOV  E,M
17 0005	23		INX  H
18 0006	EB		XCHG	    ;then into HL	
19 0007	7C		MOV  A,H    ;no left subtree?	
20 0008	B5		ORA  L      ;(pointer grounded?)	
21 0009	C40000		CNZ  PUTREE ;subtree exists, traverse it now	
22 000C	EB		XCHG	    ;restore address of original node to HL
23 000D	23		INX  H      ;skip right subtree pointer	
24 000E	23		INX  H      ;and get address of symbol narae	
25 000F	CD----		CALL PUTNAM ;output the ASCII string	
26 0012	2B		DCX  H      ;get node's right subtree pointer into DE
27 0013	5E		MOV  E,M
28 0014	2B		DCX  H
29 0015	56		MOV  D,M
30 0016	EB		XCHG	    ;then into HL	
31 0017	7C		MOV  A,H    ;no right subtree?	
32 0018	B5		ORA  L      ;(pointer grounded?)	
33 0019	C40000		CNZ  PUTREE ;subtree exists, traverse it now	
34 001C	E1		POP  H      ;restore stack	
35 001D	D1		POP  D
36 001E	C9		RET

[Listing]