Len Gorney
POB 96 RD 1
Clarks Summit PA 18411
|
Queuing Theory,
the Science of Wait Control
Part 1: Queue Representation
How many times have you waited in a line?
Do you always get to a supermarket checkout counter without having to wait?
Is the pump at the gas station always open and ready for you as you drive into the service area?
It's difficult to imagine anyone going anywhere and not having to wait in a line.
Since we're computer oriented, let's define a waiting line by its proper name - that is, a queue.
A queue is a waiting line controlled by some service mechanism.
A customer enters a queue at the tail of the queue, waits in line until he or she arrives at the head of the queue, is serviced at the head of the queue, and, finally, leaves the queue.
At the supermarket a customer pushes a cart to one of the lines formed at the checkout area and waits in a line until finally arriving at the cash register at the head of that line.
After checking out the purchases, that customer leaves the queue.
Queue Examples
Other examples of queues can be found in many areas of our everyday lives.
The supermarket checkout queue is a commercial type of queuing system.
Other commercial queues include the bank teller queue, the barbershop queue, the gas station queue, etc.
The field of transportation is not without its share of queues:
traffic lights, turnpike toll booths, airport runways, loading and unloading docks are but a few examples.
Of course, we have personal queues.
How about that shelf of books you're planning to read some day?
Let's Have Order
A queue is defined as a waiting line, and since a waiting line has both a beginning (tail) and an end (head), a queue must also have both these properties.
The head and tail idea implies that customers entering (being inserted) or leaving (being deleted) must follow a definite ordering scheme as members of the queue.
This ordering scheme is defined as the dispatching discipline of the queue.
The usual dispatching discipline of a queue is known as first in first out or FIFO.
An orderly queue exhibits this scheme.
The first person entering the queue is the first person to receive service, and the last person entering the queue is the last person to receive service.
Any person entering after the first but before the last must spend some time waiting in the queue before service may be rendered.
The first in first out discipline is but one of many ordering schemes that queues follow.
Other servicing disciplines include last in first out (eg: a stack of dishes), a priority queue, and shortest line first or longest line first (these are multiple queuing systems and will be discussed later).
Queue Representation
How can we represent a queue as part of a computer program?
The following piece of BASIC coding (a one-dimensional array) could be used to represent a queue in a computer program:
10 DIM Q(100).
A queue is nothing more than a special purpose one-dimensional array.
Just as the ordinary one-dimensional array is represented as a single row or a single column structure n locations long or deep, the queue can be represented as a single row structure n locations long.
Over and Under
When an array is dimensioned to 100 locations, the program cannot access the 104th or -36th location.
These integer values are not within the boundaries of the dimensioning statement.
If the program attempts to address out of range locations during execution of the program, an overflow or underflow condition occurs.
Overflow occurs when a location greater than that given in the dimensioning satement is addressed.
Likewise, underflow occurs when a negative subscript is given as an addressing value.
Some BASIC Interpreters allow for addressing location 0 of an array.
If an array is dimensioned to 100 locations, the actual number of legally addressable locations is 101 (counting location 0 as the first available location).
The program listings in this article do not take advantage of this extra available array location.
The first available location is always array location 1, and the last available location is equal to the integer value given in the dimensioning statement.
Let's get back to overflow and underflow as these conditions apply to queues.
If we assume that our queuing program will not address a location above or below those given in the dimensioning statement, overflow and underflow take on a somewhat different meaning.
A queue overflow occurs when the program attempts to insert an item into our queue and the queue is filled to its capacity.
Underflow in a queue structure occurs when the program attempts to delete an item from the queue but there are no items in the queue.
Queue Operations
Items in an ordinary one-dimensional array can have many operations performed on them.
A program can insert items anywhere within the array, and items can be removed from any legal location within the array.
Items can be examined and left in place or moved to any location within an array.
A queue can have only two operations performed upon its items.
The first of these allowable operations is the insertion of an item into the queue.
This insertion can be done only at the tail of the queue.
The second operation allows for deletion.
Deletion is done only at the head of the queue.
The Simple Row Queue
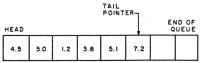
The program shown in listing 1 is a simulation of a row queue (see figure 1).
The mechanics of a row queue follow the definitions we have seen so far.
 |
|
Figure 1: Simple row queue.
This type of queue has a stationary "head" and a moving "tail."
As dato items are deleted from the head, all of the data items in the queue are moved toward the head, and the tail pointer is decremented by 1.
As more data is entered into the queue at the tail, the location of the tail pointer is incremented by one location.
|
|
Listing 1:
Simple BASIC Simulation of a row queue.
Pseudorandom number generation is done to ensure that the queue simulation works correctly as described in the text.
A sample run of the program is also shown.
|
|
|
| [BASIC-Listing] |
The row queue has its tail at location 1 of array Q, while its head is at location 5 of array Q.
The choice of these locations for tail and head is arbitrary.
I chose this scheme because it is easier to output the queue during execution of the program in a normal left-to-right reading fashion.
The head (service facility area) of the queue of listing 1 is always at location Q(5).
The tail of the queue (the location in the queue where items will be inserted) moves from location 5 toward location 0 of array Q as items are inserted into the queue.
When items are deleted, the tail of the queue moves from its present value toward location 5.
The tail of the row queue is indicated by a tail pointer (variable T).
When T is 5 the queue is empty: that is, there are no items in the queue.
When T is 0 the queue is filled to its capacity and no insertions can be made without causing an overflow condition.
To simulate the action of a queue properly, listing 1 generates pseudorandom numbers to determine queue insertion or deletion.
The importance of randomness in proper queue operation is explained later.
Before you execute the program in listing 1, run through its operations with pencil and paper.
This approach will show you how the program will run before the actual operation is simulated by the computer.
This method will also clarify the mechanics of a simple row queue operation.
The Circular Queue
A major disadvantage of our simple row queue is the fact that items must be moved toward the head of the queue after each deletion.
[Editor's Note: This is not true for all implementations of a row queue.
Often, the pointers indicating the head and tail of the row queue are moved instead of all the data inside the queue....RGAC]
The loop in line numbers 1370 through 1400 of listing 1 accomplishes this move.
If we're trying to represent a queue simulation in a computer program, why not use some programming techniques to take advantage of decreasing execution time and thereby eliminate some of the unwieldy code?
The circular queue, figure 2, is also represented as a special purpose one-dimensional array.
The simple row queue has a pointer to keep track of the location where the next item insertion was to take place.
The circular queue also has this tail pointer.
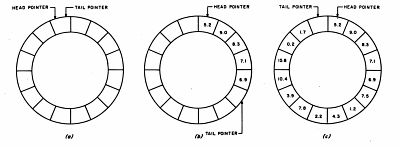 |
|
Figure 2: Circular queue in three states of use.
Figure 2a is an empty queue, in which the head pointer and the tail pointer point to the same location in the queue.
Figure 2b shows a partially filled circular queue.
The tail pointer moves ahead of the head pointer as data items are added to the queue.
As an item is deleted, the head pointer moves towards the tail pointer.
Figure 2c shows a full queue. In this state the tail pointer has caught up with the head pointer.
Note that one location in the queue will be left empty.
If this were not done, the next item added to the queue would make the head and tail pointers point to the same location, which would seem to indicate that the queue was empty.
|
The difference between the row and circular queue lies in the addition of another pointer to indicate the location of the head of the queue.
The simple row queue always has its head at the last available location of the array Q.
The circular queue structure can have its head any where within the queue.
Circular Queue Representation
The circular queue operates in the same manner as the simple row queue.
Items are still inserted into the location given as the tail point location of array Q.
The major difference is in the way which the program controls the head location of the queue.
A new variable called H (for head pointer) points to the array location which holds the item ready for deletion.
An item is inserted into the queue at the location pointed to by the tail pointer.
After this insertion, the pointer is moved by one location in readiness for another insertion.
When an item is deleted, the head pointer comes into play.
In the simple row queue, the head is always at the last available location.
In the circular queue, the head of the queue is defined by the value of the head pointer variable H.
After an item is deleted, the head pointer is moved one location toward the value of the tail pointer.
In this structure, data items remain stationary;
only the pointers vary, indicating relative positions of the tail and the head of the queue.
This queue structure is clearly advantageous when we're dealing with long queues.
If a row queue is filled to its capacity and an item is deleted, every remaining item has to be moved one at a time toward the stationary head of the row queue.
The circular queue moves the head pointer by only one location, thereby cutting program execution time.
The tradeoff is time versus space.
The circular queue program is longer than the simple row queue;
however, the time to execute the circular queue routine is shorter since the majority of code execution in the simple row queue is during the moving of the items after a delete operation.
In the circular queue, the tail pointer chases the head pointer during insertions.
During deletions, the head pointer chases the tail pointer.
When the circular queue is filled to capacity, the head and tail pointers are at adjacent locations.
No more items may be inserted simply because there is no more available space to fit an item into the queue.
An overflow condition occurs if an insertion is attempted on a filled queue.
An underflow occurs when the queue is empty and a deletion is attempted.
An empty circular queue is one in which the tail and the head pointers are at the same location in the array Q.
The program given in listing 2 simulates a circular queue.
Again, a pencil and paper method of initial execution may prove helpful.
After the mechanics of this structure are understood, then execute the program.
This completes our discussion of two different types of queues and their representation in a computer.
In part 2 we will consider queues in the world around us and fit them into the structures already developed.
|
Listing 2:
BASIC listing for a circular queue simulation.
Lines 1900 through 2100 are the insertion routine;
lines 2110 through 2270 are the deletion routine.
A sample run of the program is shown at the end of the listing.
|
|
|
| [BASIC-Listing] |
Scanned by
Werner Cirsovius
July 2003
© BYTE Publications Inc.
