|
The following article was printed in May 1985 of the magazine „Computer Language".
|
A further article referring to search by hashing.
|
|
Dynamic hashing in external searching
By Namir Clement Shammas
|
 We resume last month's discussion on hashing by presenting dynamic hashing techniques used in external searching.
We resume last month's discussion on hashing by presenting dynamic hashing techniques used in external searching.
All the techniques presented last month had a common disadvantage — the necessity of predetermined hash table sizes.
If the table is undersized, access speed will increase.
In contrast, an oversized hash table will yield an unacceptably low storage utilization.
What methods can be used to allow the hash table to increase in size as needed, and what are the criteria for this?
First, let us briefly go over the data structures involved.
We are storing search keys in file areas called buckets.
The number of keys per bucket depends on their relative sizes.
There are two types of buckets:
primary buckets, whose addresses are calculated by the hashing function, and overflow buckets.
As primary buckets fill up, additional keys are stored in the overflow buckets, forming a chain of linked lists.
Each of the linked lists contains one primary bucket and a number of overflow buckets.
The more overflow buckets, the slower the search is.
This method is called chaining.
Let us begin by focusing on what's necessary to increase the hash table size.
It depends on the average length of search (ALOS) and a maximum allowable value, ALOS_MAX.
The ALOS is calculated from:
ALOS = Sum of all(i+1) N(i)/T for i
= 0,1,2,...,max_limit
where N(0) is the number of keys in all of the primary buckets.
N(i) (for i>0) is the number of keys in the ith overflow bucket. And T is the sum of all N(i) for i = 0,1,2,...,max_limit.
Now we turn our attention to the methods used for dynamic hashing.
They are:
Linear hashing.
This method doubles the size of the hash table when the ALOS value exceeds ALOS_MAX.
If the initial table size is S0 buckets, then the size at any time, S, is S = 2d S0, where d is the doubling factor.
With the table size increasing, we are also creating a series of hashing functions with an increasing address range.
Listing 1 shows Programmer's Pseudo Listing (PPL) code for a procedure to add new keys and possibly increase the table size.
As the listing suggests, the
ALOS value is monitored as new keys are added.
When the table size is increased for the first time, the first primary bucket, BUCKET(0), is split.
This is done by taking the second half of the keys and moving them S0 addresses into the newly created bucket number S0.
The ALOS value is recalculated.
If it is still more than ALOS_MAX, the second primary bucket is split and so on until ALOS becomes less than ALOS_MAX.
Buckets are split if more than one key is in them, otherwise they are skipped.
The sequential splitting will stop before all of the primary buckets are split.
The address of the next primary bucket to be split is preserved.
It will be used the next time bucket splitting is carried out.
Once the last primary bucket is reached, the pointer is reset to point to the first bucket.
Generally, keys are moved 2d S0 addresses.
Once splitting occurs, this method will cause the primary buckets to exist in three types: split, unsplit, and new buckets.
Under these conditions, the two most recent hashing functions are needed to locate keys.
Listing 2 shows PPL code for searching in a linear hashing scheme.
As shown, we use the previous hashing function to calculate the bucket address, then check whether the bucket was unsplit.
If it is not split, we recalculate the address using the most recent hashing function.
Linear hashing with partial expansions.
This method is an improvement over the first one.
The scheme used in doubling the hash table size maintains a more uniformly distributed hash table.
We will consider doubling using two partial expansions.
Listing 3 shows PPL code for this method.
Each expansion stage adds 50% of the table size and is composed of a number of passes.
In the first stage, each pass will move selected keys from two buckets (
Figure 1) to a newly created one.
This continues in a wavelike fashion until half of the original table size is added.
The second stage is similar to the first, except that in each pass, selected keys from three buckets are moved to a new bucket.
This is carried out until the hash table size doubles.
Virtual hashing.
This method is similar to linear hashing in that it doubles the hash table size.
Its differences with linear hashing are as follows:
♦ Each primary bucket has an in-use flag orbit.
♦ The scheme for doubling the table size and splitting primary buckets is different.
♦ The entire sequence of hashing functions generated may be used to locate a bucket, starting with the most recent one and going back to previous ones.
Listing 4 shows PPL code for adding a new key to a system using virtual hashing.
First, the hashing function with a current doubling factor is used to give a bucket address.
The corresponding flag indicates whether it is occupied.
If it is vacant, the previous hashing function is used to obtain another address.
The operation continues until an occupied bucket is located.
Dynamic hashing.
This method uses three data structure components to accommodate the increase in keys.
The first component is a hash table with a predefined and fixed size.
The second is the buckets containing search keys.
No overflow buckets are needed.
The third is a dynamically growing set of trees with the task of recording the split in buckets.
The root of each tree is a hash table address.
Thus, there can be as many trees as the table size.
Initially, an equal number of buckets and hash table addresses exist, while the dynamic split trees are empty or nonexistant.
As keys are added, the hashing functions provide the address of the hash table which in turn points to the appropriate bucket.
When buckets start to fill, the hash table addresses become the roots of new split trees.
The two new tree leaves are numbered zero and one.
Leaf number zero points out to the recently filled bucket, while leaf number one points to the newly created bucket.
This scheme of creating and numbering new leaves is used to build the split trees.
Questions arise concerning how the keys are distributed during a split and how to maintain a correct search algorithm.
In other words, how do we travel through a split tree and locate the correct bucket?
One method is to use a second hashing function for the split trees.
The function is based on a pseudo random number generator yielding zeros or ones.
The search key is used to provide the seed for this function.
This will provide a consistent sequence of zeros and ones needed to traverse the split trees.
Listing 5 shows PPL code for adding a new key to this hashing method.
The same listing contains a procedure
Search_Bucket that is used to traverse through the split trees.
Modified dynamic hashing using deferred splitting.
This technique is a modification over the previous method.
A drawback of dynamic hashing is that the storage location for the split trees will quickly become large.
A way to solve this problem is to use an area for overflow buckets linked to the primary buckets.
Each primary bucket has a counter for the number of overflow buckets linked with it.
As the number exceeds a preset value, splitting occurs, following the same steps as with the previous method.
This method offers more efficient storage utilization.
Hashing techniques are very versatile methods for fast searching.
The subject is very interesting and vast.
It is worthy of additional attention and further discussions.
If you have any questions, comments, or would like to share other methods and code, please write to me in care of COMPUTER LANGUAGE, or drop me a line on the COMPUTER LANGUAGE Bulletin Board Service or CompuServe.
You may wonder what other search techniques rival the ones we have discussed.
The answer will be presented in the next issue.
We will discuss B-trees and the improved version, the B+ tree.
We will also discuss a new improvement on the B+ tree.
References
- Tremblay, J.P. and Sorenson, P.G.
An Introduction to Data Structures with Applications.
Second Edition, McGraw-Hill Book Co., New York, N.Y., 1984.
- Kruse, R.L.
Data Structures and Program Design,
Prentice-Hall, Englewood Cliffs, N.J., 1984.
| Linear hashing with partial expansions |
| 1.Size = 2SH + 1 | 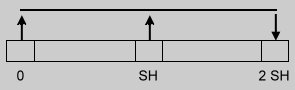 |
| 2.Size = 2SH + 2 |  |
| 3.Size = 3SH | 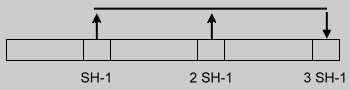 |
| 4.Size = 3SH + 1 |  |
Figure 1.
PPL code for linear hashing
PROCEDURE Add_Key1(New_Key : Key_Data)
-- All identifiers are assumed global
-- ALOS is the Average Length Of Search, and ALOS_MAX is its maximum value.
-- BUCKET() is the array of buckets
-- B is the number of keys in a primary area bucket
-- S0 is the initial size of the hash table. The actual size is calculated
-- using the following S = S0 * 2^(Doubling_factor)
-- Doubling_factor is used to expand the hash table size, and is initially
-- set equal to zero.
-- Next_Bucket is used to indicate the next bucket to be split as ALOS
-- exceeds its maximum allowable value. Initially equal zero.
BEGIN
INITIALIZE: Calculate ALOS
Update_Flag = FALSE
LOOP
BEGIN IF ALOS > ALOS_MAX THEN EXIT END IF
IF keys in BUCKET(Next Bucket) > 1
THEN
Create BUCKET(S0 + Next_Bucket)
Move last (B/2) keys from BUCKET(Next_Bucket)
to BUCKET(S0 + Next_Bucket)
Calculate new ALOS value
END IF
Next_Bucket += 1
Update_Flag = TRUE
END LOOP
TERMINATE: ADDRESS = Hash_function(New_Key,Doubling_factor,S0)
-- Update factor for new range of addresses
IF Update_Flag THEN Doubling factor +=1 END IF
END Add_Key1
|
Listing 1.
PPL code for searching in a linear hashing scheme
FUNCTION Search_Key1(Sought_Key : Key_Data; S0 : INTEGER;
BEGIN
IF Doubling_factor = 0
THEN
ADDRESS = Hash_function(Sought_Key,Doubling_factor,S0)
ELSE -- Assume key is located in a bucket that was not split
ADDRESS = Hash_function(Sought_Key,(Doubling_factor - 1),S0)
IF (ADDRESS < Next_bucket) AND (Sought_Key is not in BUCKET(ADDRESS))
THEN
ADDRESS = Hash_function(Sought_Key,Doubling_factor,S0)
END IF
END IF
RETURN (ADDRESS)
END Search_Key1
|
Listing 2.
PPL code for linear hashing with two partial expansions
PROCEDURE Expand;
-- Two-stage partial expansion scheme
-- SH = (number of initial buckets) / 2
BEGIN
INITIALIZE: SH = S0 / 2
LOOP
BEGIN FOR I = 1 TO SH
N = 2 * SH + I
Create BUCKET(N)
Move selected keys from BUCKET(I - 1) to BUCKET(N)
Move selected keys from BUCKET(SH + I - 1) to BUCKET(N)
END LOOP
TERMINATE: None
INITIALIZE: None
LOOP
BEGIN FOR I = 1 TO SH
N = 3 * SH + I
Create BUCKET(N)
Move selected keys from BUCKET(I - 1) to BUCKET(N)
Move selected keys from BUCKET(SH + I - 1) to BUCKET(N)
Move selected keys from BUCKET(2 * SH + I - 1) to BUCKET(N)
END LOOP
TERMINATE: SO *= 2 -- double table size.
END Expand
|
Listing 3.
PPL code for virtual hashing
PROCEDURE Add_Key2(New_Key : Key_Data)
-- Identifiers used are similar to those in Add_Key1.
-- Used_Flag() is an array of bits or flags to indicate if a bucket is
-- occupied by at least one key.
BEGIN
INITIALIZE: ADDRESS = Search_Key2(Sought_Key,Doubling_factor,S0,N)
LOOP
BEGIN IF BUCKET(ADDRESS) is not full THEN EXIT END IF
IF N = Doubling_factor
THEN
IF ALOS > ALOS_MAX THEN Doubling_factor += 1
ELSE -- no need to double size, yet
Obtain overflow address
END IF
END IF
Used_Flag( ADDRESS + 2^N * S0) = TRUE
N += 1
Rehash keys in BUCKET(ADDRESS) and linked overflow buckets, using N
ADDRESS = Hash_function(Sought_Key,N,S0)
END LOOP
TERMINATE: Add New_Key to BUCKET(ADDRESS)
END Add_Key2
PPL code for searching in a virtual hasing scheme
FUNCTION Search_Key2(Sought_Key : Key_Data; Doubling_factor, S0 : INTEGER;
VAR N : INTEGER) return INTEGER
BEGIN
N = Doubling_factor
INITIALIZE: ADDRESS = Hash_function(Sought_Key,N,S0)
LOOP
BEGIN IF Used_Flag(N) THEN EXIT END IF
N -= 1;
ADDRESS = Hash_function(Sought_Key,N,S0)
END LOOP
TERMINATE: RETURN(ADDRESS)
END Search_Key2
|
Listing 4.
Adding keys to a dynamic hashing scheme
PROCEDURE Add_Key3(New_Key : Key_Data)
-- Add a new key using dynamic hashing scheme
BEGIN
ADDRESS = Hash_function(New_Key,Hash_Table_Size)
IF Tree_ptr(ADDRESS) is nul
THEN -- Hash table address points to bucket directly
Process_Bucket
ELSE -- Hash table address is a root for a split tree
Search_Bucket -- obtain bucket address
Process_Bucket
END IF
END Add_Rey3
----------------------------------------------------------------------
PROCEDURE Search_Bucket
-- Search for a bucket by traversing a split tree
BEGIN
INITIALIZE: ROOT = Hash_Ptr(ADDRESS)
LOOP <Traverse>
BEGIN
ADR = Hash_function2(New_Key)
IF Leaf(ROOT ADR).Type is terminal THEN EXIT <Traverse> END IF
ROOT = Leaf(R0OT,ADR).Ptr
END LOOP <Traverse>
TERMINATE: ADDRESS = Leaf(ROOT,ADR).Ptr
END Search_Bucket
PROCEDURE Process_Bucket
BEGIN
READ Bucket_File,ADDRESS,BUCKET
IF BUCKET.Count_Key = MAX_KEY
THEN -- BUCKET(ADDRESS) is full
Split_Bucket
ELSE -- Simply add key
BUCKET.Count_Key += 1
BUCKET.Key(BUCKET.Count_Key) = New_Key
END IF
END Process_Bucket
PROCEDURE Split_Bucket
BEGIN
Num_Bucket += 1
BUCKET.Key(MAX_KEY+1) = New_Key
INITIALIZE: BUCKET.Count_Key = 0
NEWBUCKET.Count_Key = 0
LOOP
BEGIN FOR i = 1 to MAX_KEY + 1
ADR = Hash_Function2(BUCKET.Key(i)) -- 0/1 function
IF ADR = 0
THEN BUCKET.Count_Key += 1
BUCKET.Key(BUCKET.Count_Key) = BUCKET.Key(i)
ELSE
NEWBUCKET,Count_Key += 1
NEWBUCKET.Key(BUCKET Count_Key) = BUCKET.Key(i)
END IF
END LOOP
TERMINATE: WRITE Bucket_File,ADDRESS,BUCKET
WRITE Bucket_File,Num_Bucket,NEWBUCKET
Create leaves in memory and link them hash table
Set leaf pointers to ADDRESS and Num_Bucket
END Split_Bucket
|
Listing 5.
|
HTML customization by
Werner Cirsovius
January 2015
© CL Publications




