The following article was printed in February 1980 of the magazine „Microcomputing".

This article demonstrates computation of reals using integers, here referred to square roots.

An article calculating sine, cosine, square and square root functions using integer maths will be found here. More articles calculating sine, cosine functions using integer maths will be found here and here.

Tom Crawford
50 Brentwood Dr.
Stoney Creek, Ontario
Canada L8G 2W8

Tiny BASIC Square Root Routine

Story on how this author got squared away with Tiny BASIC.

Recently I spent three long evenings keying Tom Pittman's1 Tiny BASIC into my 1802 system. After making several copies on cassette tape, I prepared to bring Tiny to life. Amazingly, it worked the first time. Several short programs served to satisfy me that Tiny BASIC was fully operational. (The first program was a counting and printing loop – with no termination! It provided a good test of the BREAK key on my keyboard.)

It was time to get down to serious business. I began searching all the BASIC games books I had accumulated, looking for demonstration programs I could run. Remember, Tiny lacks floating point numbers, character manipulation, SQR(), data statements, dimension statements and a few other things.

This weeded out quite a few programs I would have liked to try, but I still managed to fill several cassettes with games such as Tic-Tac-Toe, Acey-Ducey, Moon-Lander... but wait, I didn't notice the use of the SQR() function in Moon-Lander until I was three-quarters of the way through "hunt and pecking" it into my system. I wasn't about to waste all that effort, so obviously the only thing to do was to write a square root routine, right?

The Routine

At this point my old four-function calculator proved useful again. The hardware had long since disappeared into various projects, but the instruction manual was still around and contained an elegant little algorithm for finding square roots. All that I had to do was program this into a little subroutine.

The algorithm is shown in Example 1, where x is the number we wish to find the square root of, and Y is an approximate square root. We simply code this into a loop and go around the loop until (Y_n+1−Y_n) is less than the error we are willing to accept. Since Tiny BASIC works in Integer, it is acceptable to use Y_n+1=Y_n to terminate the loop.

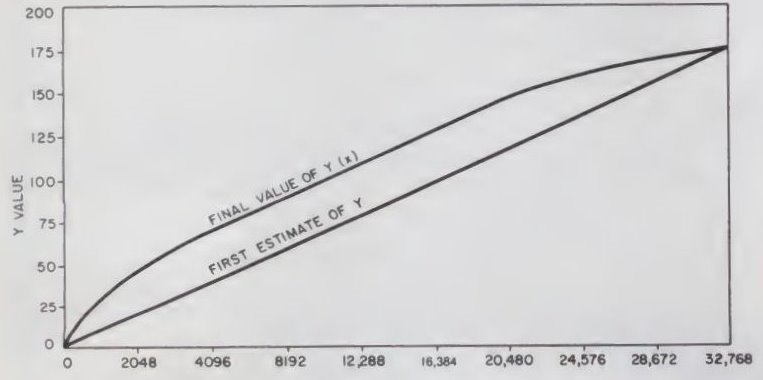Fig. 1. Tiny BASIC Square Root routine. Root of x = Y_n+1 = Y_n/2 + x/(2*Y_n), where the first estimate of Y = x/182 + 2.

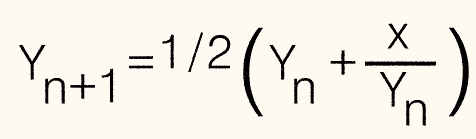Example 1.

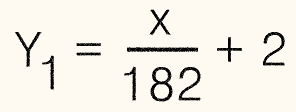Example 2.

The only other thing we need before we can code this is the initial estimate of Y, Y₁. The closer Y₁ is to the final value of Y, the faster the square root function will work. Although using Y = a constant (say 100) will work, I chose to use a straightline approximation of the root (see Example 2).

The term 2 prevents Y_n from becoming 0, which will result in a divide by error in the first equation. The factor 182 results from consideration of the useful range of the routine, and is approximately √32,767 (see Fig. 1).

Note that this routine will not handle √1, but this can be tested for and handled separately. Thus the effective range of the square root routine will be: 1≤ x ≤32,767.

At this point the routine was coded up and used in Moon-Lander with no apparent problem. The routine is shown in Example 3.

1000 REM       SQUARE ROOT ROUTINE. RETURNS ROOT OF A IN 
1010 REM       B. WORKSPACE IS C 
1020 IF A>1 GOTO 1050 
1030 B = 1 
1040 RETURN 
1050 B = A/182 + 2 
1060 C = (B + A/B)/2 
1070 IF B = C RETURN 
1080 B = C 
1090 GOTO 1060

Example 3.

Modification

Unfortunately, there are still two problems with this routine. First, for some values of A, such as 8, the condition B = C is never satisfied. The value of B in the case of A = 8 will oscillate between 2 and 3. This is caused by the truncation error in line 1060 of Example 3, where C is calculated. It is necessary to modify the routine to watch for this situation, pick one of the two values as the root and then return.

The second problem is that this routine does not return the correct root for many of the "perfect square" numbers, such as 16 and 64! It will be necessary to correct for this truncation by rounding up the result C if the remainder exceeds .5. It is sufficient to check the remainder of the second term only in line 1060.

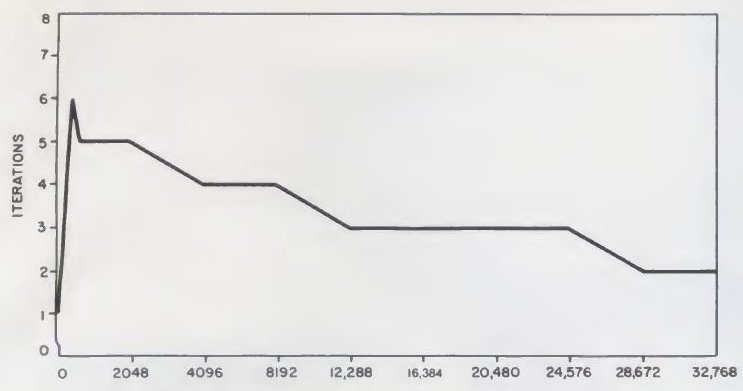Fig. 2. Number of iterations of the algorithm required over the range 0<x≤32,7676.

1000 REM       SQUARE ROOT ROUTINE. RETURNS ROOT OF A IN 
1010 REM       B. WORKSPACE IS C AND D.
1020 IF A>1 GOTO 1050
1030 B = 1 
1040 RETURN
1050 B = A/182 + 2
1060 D = 0 
1070 C = (B + A/B)/2
1074 REM CHECK IF C SHOULD BE ROUNDED UP 
1075 IF (A - A/(2*B)*B*2)>B C = C + 1
1080 IF B = C RETURN
1085 REM CHECK FOR OSCILLATION OF RESULT
1090 IF (B-C) = D GOTO 1130 
1100 D = C-B
1110 B = C 
1120 GOTO 1070
1130 REM PICK THE LARGER OF B OR C THEN RETURN
1140 IF B>C RETURN
1150 B = C
1160 RETURN

Example 4.

[Version for Microsoft-MBASIC with main part for number input. This version uses the operator / for division. Before I found another version in the internet I planned to implement the routine in assembler. Just for curiosity I changed the operator / against \ (integer division). But this version was buggy. (E.g. SQR(16) lead to 5 instead of 4, SQR(36) to 7, SQR(64) to 9) The TURBO-PASCAL version was buggy too, of course.
Deleting line 1075 finally yielded into the correct results. (The ultimate version written in BASIC and PASCAL)]

The modified routine is shown in Example 4. Fig. 2 gives some indication of the speed of the algorithm for various input values.

1. My very first computer was a COSMAC ELF (http://www.cirsovius.de/COSMAC/ELF-II-en.html) running TINY BASIC, too. For the INTEL 8080 the "PaloAlto Tiny Basic" by Lee-Chen Wang does exist (here as tar file). It uses the RST 1..7 instructions. Unfortunately RST 7 is used as interrupt entry on the Joyce. I modified the Z80 source moving the short RST routines into the CP/M TPA.