| Hagen Völzke |
Teil 4: Die Konvertierungsroutinen
Mit den Grundrechenarten ist ein Fließkommapaket noch nicht fertig - schließlich will man die Zahlen ja nicht in diesem Format eingeben.
Dieser Teil behandelt die Konvertierung zwischen Fließkommazahlen und anderen Darstellungen, zunächst der Integerdarstellung.
|
log() der Logarithmus zur Basis Zehn.
Als Ergebnis erhalten wir
n = 7,2247...
Wir müssen n immer zur nächsten kleineren Zahl abrunden, um die Zahl der genauen Dezimalstellen zu erhalten, da man Bruchteile von Stellen ja nicht ablesen kann.
„Genau" sind in diesem Fall also höchstens sieben Dezimalstellen.
Im Fall einer double-precision-Fließkommazahl mit 52-Bit-Mantisse ergibt sich:
| n | = | log(252); |
| = | 15.6535... |
|
INCLUDE-Anweisungen eingebunden werden, da sie einige Definitionen aus diesen Listings mitbenutzen.
f_ltof bewirkt die Konvertierung von Long-Integer-Zahlen zur Fließkomma-Darstellung.
Standardmäßig werden lange Integerzahlen, also 32-Bit Zahlen, unterstützt.
Die Konvertierung einer Integer-Zahl in eine Fließkommazahl bereitet kaum Probleme.
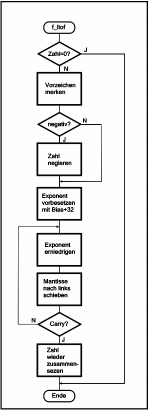
Dazu betrachten wir das Flußdiagramm in Bild 4.
 |
| Bild 4. Flußdiagramm zur Konvertierung LONG-INTEGER TO FLOAT |
f_ltof-Funktion beim Prozessor 68000 mit nur 16 CPU-Befehlen auskommt, füllt das Programm für den Z80 schon wieder eine ganze Seite.
Insbesondere die Abfrage auf Null sowie die Negierung der Integerzahl ergeben schon längere Programmsequenzen, die das Listing zu einem großen Teil füllen.
f_ftol kehrt die Operation der Funktion f_ltol gerade um:
aus einer Fließkommazahl wird wieder eine Integerzahl gemacht.
Diese Umkehrung ist allerdings nicht vollständig, denn eine Fließkommazahl verwendet lediglich eine 24-Bit-Mantisse, während eine Integerzahl 31 Bit lang ist (plus 1 Bit Vorzeichen).
Je nach Größe der Integerzahl werden also bei der Konvertierung von Integer in Fließkomma bis zu 7 Bit einfach abgeschnitten, die natürlich bei einer späteren Rückwandlung nicht mehr vorhanden sind.
Die Funktion f_ftol extrahiert zunächst den Exponenten der Fließkommazahl und subtrahiert anschließend den Bias.
(Siehe auch Flußdiagramm Bild 5.)
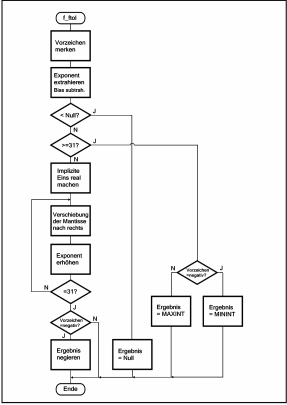 |
| Bild 5. Flußdiagramm zur Konvertierung FLOAT TO LONG-INTEGER |
MAXINT (bzw. MININT) zurückgegeben.
Auch die Funktion f_ftol benötigt eine Schiebeschleife.
In dieser werden die Bits der Mantisse wieder rechtsbündig positioniert, um den korrekten Integerwert herzustellen.
Am Schluß muß noch das Ergebnis negiert werden, falls die Fließkommazahl negativ war.
Integerwerte werden stets im Zweierkomplement dargestellt, Fließkommawerte dagegen durch einen Absolutbetrag (Mantisse) und ein getrenntes Vorzeichenbit.
f_mul2 wird mit zwei Parametern aufgerufen.
Der erste Parameter ist eine Fließkommazahl, der zweite ein Integerwert, der den Exponenten der Zweierpotenz angibt.
Zum Aufruf drei Beispiele:
f_mul2(fpzahl,1) ≡ fpzahl * (21) = fpzahl * 2f_mul2 prüft zunächst ab, ob die Fließkommazahl Null ist.
Dann ist auch das Ergebnis Null, und es kann sofort abgebrochen werden.
Andernfalls wird nun der Exponent der Fließkommazahl extrahiert.
Nun muß leider eine Fallunterscheidung vorgenommen werden, denn die Fließkommazahl könnte ja denormalisiert sein.
Dann nämlich muß bei der Multiplikation zunächst die Zahl normalisiert werden, bevor der Exponent verändert werden darf.
Ein ähnlicher Fall tritt bei der Division auf:
es entsteht ein Exponenten-Unterlauf, und das Ergebnis muß denormalisiert werden.
Beim Durchlauf mit normalisierten Zahlen werden lediglich die beiden Exponenten addiert, und das Ergebnis wird wieder zusammengesetzt.
Die Sonderbehandlungen, die das Listing wieder etwas in die Länge ziehen, sind nur für die denormalisierten Zahlen von Belang und werden auch nur für diese durchlaufen.
Gegenüber der normalen Fließkommamultiplikation spart man sich die Mantissenmultiplikation sowie fast alle anderen Behandlungen der Mantisse.
Über- und Unterlauf müssen natürlich auch abgefangen werden und produzieren jeweils MAXFLOAT bzw. Null.
Alternativ kann auch hier wieder eine Fehlerbehandlung eingesetzt werden.
Der Geschwindigkeitsgewinn gegenüber der normalen Multiplikation ist sehr hoch.
Eingescanned von
Werner Cirsovius
September 2004
© Franzis' Verlag