|
Im Magazin „MC" wurde im Oktober 1985 der folgende Artikel abgedruckt.
|
Ein Artikel zur Bit-Korrektur bei fehlerhafter Datenübertragung, Hilfroutinen geschrieben ursprünglich für die CPU 6502, hier Routinen für die Z80.
Im Gegensatz zur herkömmlichen Erzeugung des Hamming-Bytes wird dieses hier nicht binär sondern als druckbares Zeichen erzeugt.
|
|
Ein falsches Bit ist kein Problem
Datenübertragung mit Fehlerkorrektur
Fehlererkennung ist gut - Fehlerkorrektur ist besser!
Der folgende Vorschlag erlaubt eine automatische Korrektur von Einzelbit-Fehlern sowie die Erkennung von Mehrbit-Fehlern ohne viel Aufwand und läßt sich z.B. zur Übertragung von Programmen per Telefon einsetzen.
Fehlerkorrigierende Übertragungsverfahren lassen sich überall dort sinnvoll einsetzen, wo Fehler nie gehäuft auftreten, sondern nur ab und zu.
Je häufiger man Fehler zulassen und automatisch korrigieren will, desto mehr Prüfzeichen muß man zusätzlich zur eigentlichen Information übertragen (Redundanz).
Der Informatiker Hamming hatte die theoretischen Grundlagen für fehlerkorrigierende Übertragungsverfahren längst geschaffen, bevor es eine Anwendung dafür gab;
heute nennt man die zusätzlichen Prüfbits ihm zu Ehren Hamming-Bits.
Sieben Bits als Matrix
Es gibt sehr unterschiedliche Möglichkeiten der Korrektur-Bit-Gewinnung;
sie alle beruhen im Prinzip aber darauf, die zu übertragenden Datenbits als Matrix aufzuschreiben und aus deren Zeilen und Spalten mehrere Paritätsbits aufzusummieren.
Die mehr oder weniger willkürlich angenommene Bitmatrix des hier verwendeten Verfahrens zeigt Bild 1.
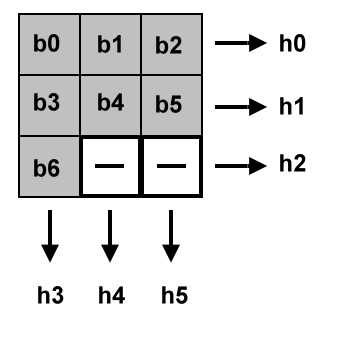
|
Bild 1. Aus den sieben Datenbits b0...b6 werden die sechs Prüfbits h0...h5 gewonnen
|
Aus den für eine ASCII-Textübertragung nötigen sieben Datenbits b0...b6 werden sechs Korrektur-Bits h0...h5 gewonnen, indem für jede Zeile und Spalte der Matrix festgestellt wird, ob die Summe der Bits gerade oder ungerade ist.
Die Möglichkeit der Fehlerkorrektur ergibt sich aus folgender Überlegung:
Wenn ein Datenbit falsch übertragen wird, so wird der Rechner auf der Empfangsseite ein vom empfangenen in zwei Bits abweichendes Prüfbyte ermitteln.
Diese zwei Bits geben unter Zuhilfenahme der Matrix die Nummer des falschen Datenbits an, das dann nur noch invertiert werden muß.
Wird im Prüfbyte selbst ein (und nur ein) Bit falsch übertragen, so stellt der Empfänger fest, daß dies kein sinnvoller Matrixcode ist, und ignoriert diesen Fehler einfach.
Zwei falsche Bits werden zumindest in den meisten Fällen erkannt, können aber nicht mehr korrigiert werden.
Welche Ergebnisse beim bitweisen Vergleich gesendeter Codes auftreten können, geht aus Bild 2 hervor;
es sind logischerweise genau sieben, entsprechend der Anzahl der Datenbits des zu korrigierenden Zeichens.
|
Bild 2. Aus dieser Zahlenmatrix kann man empfangsseitig ermitteln, welches Datenbit falsch ist und invertiert werden muß
|

|
Entsprechend h0...h5 trägt der hier verwendete Algorithmus Zweierpotenzen für die Spalten und Zeilen der Matrix ein und addiert sie für jede Bitposition.
Wird beispielsweise b4 (das Bit in der Mitte der Matrix) falsch übertragen, so weicht der empfangsseitig ermittelte Hamming-Code vom übertragenen in h1 und h4 ab.
21 + 24 ergibt 2 + 16 = 18.
Der Rechner braucht nun lediglich in einer Tabelle wie in Bild 2 nachzusehen, welches Bit (nämlich b4) er invertieren muß.
Nur druckende Codes
Bei der Übertragung wird jedem Textzeichen ein zusätzliches Zeichen mit den sechs Korrektur-Bits angehängt.
Da also nur sechs der sieben ASCII-Bits ausgenutzt werden, kann man dafür sorgen, daß alle Prüfzeichen in den Bereich der „druckenden" Codes fallen, so daß keine Steuerzeichen (hex 00...1F und 7F) generiert werden.
Das ist recht einfach, indem man zu jedem Prüf-Byte hex 20 addiert, so daß die Prüfzeichen im Bereich hex 20...5F liegen.
Das ist wichtig, weil viele DFÜ-Programme einerseits die meisten Steuerzeichen sperren, andererseits bestimmte Codes zu unerwünschten Effekten im Rechner fuhren würden.
Von dieser Überlegung ausgehend entstand ein 6502-Programm, das im Originalartikel abgedruckt war.
[Das 6502 Listing kann hier dargestellt werden]
Fehlertolerante DFÜ
Für die Z80 Version stehen im Wesentlichen zwei Routinen zur Verfügung:
fsend:
Aus dem im Akku stehenden Zeichen wird das Hamming-Byte berechnet.
Dieses Byte steht bei Ende der Routine im Akku, das Zeichen ist in das Register C kopiert.
fempf:
Aus dem Zeichen im Register C und dem Hamming-Byte im Akku wird im Fehlerfall versucht, das Zeichen zu korrigieren.
Am Ende steht das Zeichen im Akku und im Register B.
Ist eine Korrektur nicht möglich, so ist die Carry Flag gesetzt und im Akku steht ein Fragezeichen.
|
|
| [Listing] |
| Z80-Programm zum Senden und Empfangen eines Zeichens mit automatischer Fehlerkorrektur
|
Das nachstehende Testprogramm nimmt Textzeilen entgegen, bis eine Leerzeile eingegeben wird.
Danach werden aus den einzelnen Zeichen die Hamming-Bytes gebildet.
Der Wert des Zeichens wird um 1 erhöht und es wird nun versucht, eine Korrektur durchzuführen.
Im Extremfall kann eine Abweichung von allen sieben möglichen Bits stattfinden.
Dies ist z.B. der Fall beim Zeichen
?:
| ASCII Zeichen | ? |
| Hexwert | 0x3F |
| Binärwert | 0111111 |
| 1 addieren | 0000001 |
| Ergibt Binärwert | 1000000 |
| Hexwert | 0x40 |
|
|
| [Listing] |
| Z80-Testprogramm
|
Praktische Erfahrungen
[Dieser Absatz bezieht sich auf den Originalartikel]
Die Wirksamkeit der fehlerkorrigierenden Datenfernübertragung hängt sehr stark davon ab, welcher Art die Fehler sind, die typischerweise auf der Leitung auftreten.
Handelt es sich vorwiegend um sehr kurze Knack-Geräusche (z.B. Schaltspitzen bei Ortsgesprächen), so werden die resultierenden Bitfehler korrigiert.
Sogenannten Bündelstörungen, bei denen mehrere aufeinanderfolgende Bits gestört sind, ist das Verfahren naturgemäß nicht gewachsen;
sie treten bei Ferngesprächen manchmal auf.
Verfolgt man die Übertragung am Bildschirm, so sieht man, daß nach der ersten Zeile jede mit einem B beginnt;
ebenso steht nach jedem Leerraum ein B (Bild 4):
Das ist zufällig sowohl der Korrektur-Code für Return als auch für Space.
(Notwendigerweise gibt es diese Mehrdeutigkeit des Prüfzeichens, da ja sechs Hamming-Bits aus sieben Datenbits erzeugt werden.)
Das B nach dem letzten Return sollte man nicht löschen, weil sonst die letzte Zeile nicht korrekt abgeschlossen wird.
Dies ist ein Textbei-
spiel, an dem deutlich
wird, da_ die fehler-
korrigierende \bertra-
gung doppelt so lange
dauert.
|
Bild 4. Ein kurzer Text ohne (oben)
und mit Prüfzeichen (unten)
|
DMiMe&sD BiMsDt= Be&iMn4 BT_e&xVt=b_e&iM-
BsDp\iMe&l%,) BaGn4 Bd/e&m, Bd/e&u4t=l%iMcVhD
Bw%iMrMd/,) Bd/aG_M Bd/iMe& Bf>e&hDl%e&rM-
Bk\o=rMrMiMg7iMe&rMe&n4d/e& B\Ub_e&rMt=rMaG-
Bg7u4n4g7 Bd/o=p\p\e&l%t= BsDo= Bl%aGn4g7e&
Bd/aGu4e&rMt=.8
B
|
Eingescanned von
Werner Cirsovius
September 2007
© Franzis' Verlag


